题目内容
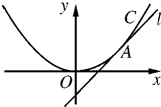 如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.(1)求实数b的值;
(2)已知圆P经过A点且始终与抛物线C的准线相切,求圆P的圆心的轨迹方程,并说明其是什么曲线?.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)直线与抛物线方程联立化为x2-4x-4b=0.由于直线l与抛物线相切,令△=0,即可解得.
(2)由于圆P经过A点且始终与抛物线C的准线相切,可得|PA|=|y+1|,利用两点之间的距离公式即可得出.
(2)由于圆P经过A点且始终与抛物线C的准线相切,可得|PA|=|y+1|,利用两点之间的距离公式即可得出.
解答:
解:(1)由
,得x2-4x-4b=0.
∵直线l与抛物线相切,
∴△=(-4)2-4×(-4b)=0,解得b=-1.
(2)由(1)已知A的坐标为(2,1),
设P(x,y).
∵圆P经过A点且始终与抛物线C的准线相切,
∴|PA|=|y+1|
∴
=|y+1|
∴圆心轨迹(x-2)2=4y是抛物线.
|
∵直线l与抛物线相切,
∴△=(-4)2-4×(-4b)=0,解得b=-1.
(2)由(1)已知A的坐标为(2,1),
设P(x,y).
∵圆P经过A点且始终与抛物线C的准线相切,
∴|PA|=|y+1|
∴
| (x-2)2+(y-1)2 |
∴圆心轨迹(x-2)2=4y是抛物线.
点评:本题考查了抛物线的标准方程及其性质、直线与抛物线的位置关系、圆的方程、两点之间的距离公式,考察了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若x∈(2,4),则下列结论正确的是( )
| A、2x>x2>log2x |
| B、x2>log2x>2x |
| C、log2x>x2>2x |
| D、x2>2x>log2x |
已知F1,F2是椭圆的左,右焦点,以右焦点F2为圆心的圆过F1且与右准线相切,则椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知椭圆:
+x2=1,过点P(
,
)的直线与椭圆相交于A,B两点,且弦AB被点P平分,则直线AB的方程为( )
| y2 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、9x-y-4=0 |
| B、9x+y-5=0 |
| C、2x+y-2=0 |
| D、2x-y+2=0 |