题目内容
在△ABC中,角A,B,C的对边分别是a,b,c,且a>c.已知
•
=2,cosB=
,b=3.
(1)求a和c的值;
(2)求cosC的值.
| BA |
| BC |
| 1 |
| 3 |
(1)求a和c的值;
(2)求cosC的值.
考点:余弦定理,平面向量数量积的运算
专题:解三角形
分析:(1)已知等式利用平面向量的数量积运算法则变形,把cosB的值代入求出ac=6,由余弦定理列出关系式,整理求出a+c=5,联立求出a与b的值即可;
(2)由cosB的值求出sinB的值,再由b与c的值,利用正弦定理求出sinC的值,即可确定出cosC的值.
(2)由cosB的值求出sinB的值,再由b与c的值,利用正弦定理求出sinC的值,即可确定出cosC的值.
解答:
解:(1)∵
•
=accosB=2,cosB=
,
∴ac=6①,
∵b=3,
∴由余弦定理得:b2=a2+c2-2accosB=a2+c2-
ac=(a+c)2-
ac,即9=(a+c)2-16,
整理得:a+c=5②,
联立①②得:a=2,c=3(不合题意,舍去),
则a=3,c=2;
(2)由cosB=
,得到sinB=
,
∵b=3,c=2,
∴由正弦定理
=
得:sinC=
=
=
,
则cosC=
.
| BA |
| BC |
| 1 |
| 3 |
∴ac=6①,
∵b=3,
∴由余弦定理得:b2=a2+c2-2accosB=a2+c2-
| 2 |
| 3 |
| 8 |
| 3 |
整理得:a+c=5②,
联立①②得:a=2,c=3(不合题意,舍去),
则a=3,c=2;
(2)由cosB=
| 1 |
| 3 |
2
| ||
| 3 |
∵b=3,c=2,
∴由正弦定理
| b |
| sinB |
| c |
| sinC |
| csinB |
| b |
2×
| ||||
| 3 |
4
| ||
| 9 |
则cosC=
| 7 |
| 9 |
点评:此题考查了正弦、余弦定理,平面向量的数量积运算,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
若x∈(2,4),则下列结论正确的是( )
| A、2x>x2>log2x |
| B、x2>log2x>2x |
| C、log2x>x2>2x |
| D、x2>2x>log2x |
下列选项中,可作为函数y=f(x)的图象的是( )
A、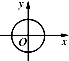 |
B、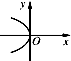 |
C、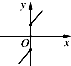 |
D、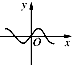 |
设集合M={x|x2+2x-a=0},若M非空,则实数a的取值范围是( )
| A、a≤-1 | B、a≥-1 |
| C、a≤1 | D、a≥1 |