题目内容
已知函数f(x)=ax3ex-1+bx3+c在x=1处取得极值2b+c+7,a,b,c为常数,
(1)试确定a,b的值;
(2)当x∈[-4,+∞)时,讨论函数f(x)的单调区间;
(3)若存在x>0,使得不等式f(x)≤c2-2c-1成立,求c的取值范围.
(1)试确定a,b的值;
(2)当x∈[-4,+∞)时,讨论函数f(x)的单调区间;
(3)若存在x>0,使得不等式f(x)≤c2-2c-1成立,求c的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)利用导数与函数极值的关系列出方程组即可求出a,b的值;
(2)由(1)得f(x)=3x3ex-1-4x3+c,f′(x)=9x2ex-1+3x3ex-1-12x2=3x2[(3+x)ex-1-4],利用导数即可求得函数的单调区间;
(3)由(2)可知,当x=1时,f(x)min=-1+c,则有-1+c≤c2-2c-1,解得即可.
(2)由(1)得f(x)=3x3ex-1-4x3+c,f′(x)=9x2ex-1+3x3ex-1-12x2=3x2[(3+x)ex-1-4],利用导数即可求得函数的单调区间;
(3)由(2)可知,当x=1时,f(x)min=-1+c,则有-1+c≤c2-2c-1,解得即可.
解答:
解:(1)f′(x)=3ax2ex-1+ax3ex-1+3bx2,
∵f(x)=ax3ex-1+bx3+c在x=1处取得极值2b+c+7,
∴
即
解得a=3,b=-4.
(2)由(1)得f(x)=3x3ex-1-4x3+c,
f′(x)=9x2ex-1+3x3ex-1-12x2=3x2[(3+x)ex-1-4],
∴当-4≤x≤1时,f′(x)≤0,当x>1时,f′(x)>0,
∴函数f(x)在[-4,1]上是减函数,在(1,+∞)上是增函数.
(3)由(2)可知,当x=1时,f(x)min=-1+c,
∴若存在x>0,使得不等式f(x)≤c2-2c-1成立,则有,
-1+c≤c2-2c-1,解得c≤0或c≥3.
∵f(x)=ax3ex-1+bx3+c在x=1处取得极值2b+c+7,
∴
|
|
(2)由(1)得f(x)=3x3ex-1-4x3+c,
f′(x)=9x2ex-1+3x3ex-1-12x2=3x2[(3+x)ex-1-4],
∴当-4≤x≤1时,f′(x)≤0,当x>1时,f′(x)>0,
∴函数f(x)在[-4,1]上是减函数,在(1,+∞)上是增函数.
(3)由(2)可知,当x=1时,f(x)min=-1+c,
∴若存在x>0,使得不等式f(x)≤c2-2c-1成立,则有,
-1+c≤c2-2c-1,解得c≤0或c≥3.
点评:本题主要考查利用导数研究函数的单调性、极值、最值等知识,考查学生恒成立问题的等价转化能力,属于中档题.

练习册系列答案
相关题目
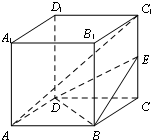 如图,在边长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点.
如图,在边长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点.