题目内容
设全集U=R，集合A={x|-1＜x＜4}，B={y|y=x+1，x∈A}，试求∁UB，A∪B，A∩B，A∩（∁UB），（∁U A）∩（∁UB）．
考点：交、并、补集的混合运算
专题：集合
分析：根据y=x+1，x∈A={x|-1＜x＜4}求出集合B，再由补集、交集、并集的运算依次求出即可．
解答：
解：由条件得，y=x+1，x∈A={x|-1＜x＜4}，
所以B={y|0＜y＜5}，则∁UB={y|y≤0或y≥5}=（-∞，0]∪[5，+∞），
A∪B={y|-1＜y＜5}=（-1，5），A∩B={y|0＜y＜4}=（0，4），
A∩（∁UB）={y|-1＜y≤0}，
又（∁U A）={y|y≤-1或y≥4}=（-∞，-1]∪[4，+∞），
所以（∁U A）∩（∁UB）={y|y≤-1或y≥5}=（-∞，-1]∪[5，+∞）．
所以B={y|0＜y＜5}，则∁UB={y|y≤0或y≥5}=（-∞，0]∪[5，+∞），
A∪B={y|-1＜y＜5}=（-1，5），A∩B={y|0＜y＜4}=（0，4），
A∩（∁UB）={y|-1＜y≤0}，
又（∁U A）={y|y≤-1或y≥4}=（-∞，-1]∪[4，+∞），
所以（∁U A）∩（∁UB）={y|y≤-1或y≥5}=（-∞，-1]∪[5，+∞）．
点评：本题考查了交、并、补集的混合运算，熟练掌握交、并、补集的运算是解题的关键，属于基础题．
练习册系列答案
寒假学与练系列答案
相关题目
已知M={x∈R|x≥2
}，a=π，有下列四个式子：①a∈M；②{a}?M；③a⊆M；④{a}∩M=π，其中正确的是（ ）
| 2 |
| A、①② | B、①④ | C、②③ | D、①②④ |
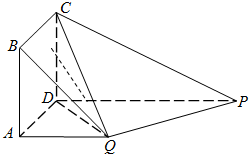在如图所示的多面体中，四边形ABCD为正方形，四边形ADPQ是直角梯形，AD⊥DP，CD⊥平面ADPQ，AB=AQ=| 1 |
| 2 |
（1）求证：PQ⊥平面DCQ；
（2）若AQ=2，求四面体C-BDQ的体积．
若U={1，2，3，4，5，6，7}，A={3，4，6，7}，B={3，5，6，7}，则∁U（A∩B）=（ ）
| A、{1，2，4，5} |
| B、{2，6，8} |
| C、{1，3，5，7} |
| D、{1，2} |