题目内容
求下列函数的定义域:
(1)y=
;
(2)y=
.
(1)y=
| 3 | ||
1-
|
(2)y=
| (x+1)0 |
| |x|-x |
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用
分析:(1)由不等式组
解得x≤1且x≠0,写成集合即为定义域;
(2)由不等式组
解得x<0且x≠-1写成集合即为定义域;
|
(2)由不等式组
|
解答:
解:(1)要使函数y=
有意义,需要
解得x≤1且x≠0
∴y=
的定义域为{x|x≤1且x≠0}
(2)要使函数y=
有意义,需要
解得x<0且x≠-1
∴y=
的定义域为{x|x<0且x≠-1}
| 3 | ||
1-
|
|
∴y=
| 3 | ||
1-
|
(2)要使函数y=
| (x+1)0 |
| |x|-x |
|
∴y=
| (x+1)0 |
| |x|-x |
点评:本题考查函数的定义域及其求法,是基础题,解题时要认真审题,仔细解答.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
下列集合中,只有一个子集的集合为( )
| A、{x|x2≤0} |
| B、{x|x3≤0} |
| C、{x|x2<0} |
| D、{x|x3<0} |
已知M={x∈R|x≥2
},a=π,有下列四个式子:①a∈M;②{a}?M;③a⊆M;④{a}∩M=π,其中正确的是( )
| 2 |
| A、①② | B、①④ | C、②③ | D、①②④ |
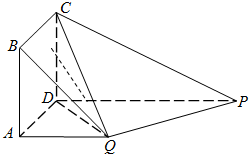 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=