题目内容
已知关于x的一元二次方程x2-(2k+1)x+k2+2k=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得x1•x2-x12-x22≥0成立?若存在,请求出k的值;若不存在,请说明理由.
(1)求实数k的取值范围;
(2)是否存在实数k使得x1•x2-x12-x22≥0成立?若存在,请求出k的值;若不存在,请说明理由.
考点:一元二次方程的根的分布与系数的关系
专题:综合题,不等式的解法及应用
分析:(1)利用[-(2k+1)]2-4(k2+2k)≥0,即可求实数k的取值范围;
(2)假设存在实数k使得x1•x2-x12-x22≥0成立,利用韦达定理,代入计算,即可得出结论.
(2)假设存在实数k使得x1•x2-x12-x22≥0成立,利用韦达定理,代入计算,即可得出结论.
解答:
解:(1)∵原方程有两个实数根,
∴[-(2k+1)]2-4(k2+2k)≥0…(1分)
∴4k2+4k+1-4k2-8k≥0
∴1-4k≥0,…(3分)
∴k≤
.
∴当k≤
时,原方程有两个实数根. …(6分)
(2)假设存在实数k使得x1•x2-x12-x22≥0成立.
∵x1,x2是原方程的两根,
∴x1+x2=2k+1,x1•x2=k2+2k. …(8分)
由x1•x2-x12-x22≥0,
得3x1•x2-(x1+x2)2≥0.
∴3(k2+2k)-(2k+1)2≥0,整理得:-(k-1)2≥0,
∴只有当k=1时,上式才能成立. …(10分)
又由(1)知k≤
,
∴不存在实数k使得x1•x2-x12-x22≥0成立. …(12分)
∴[-(2k+1)]2-4(k2+2k)≥0…(1分)
∴4k2+4k+1-4k2-8k≥0
∴1-4k≥0,…(3分)
∴k≤
| 1 |
| 4 |
∴当k≤
| 1 |
| 4 |
(2)假设存在实数k使得x1•x2-x12-x22≥0成立.
∵x1,x2是原方程的两根,
∴x1+x2=2k+1,x1•x2=k2+2k. …(8分)
由x1•x2-x12-x22≥0,
得3x1•x2-(x1+x2)2≥0.
∴3(k2+2k)-(2k+1)2≥0,整理得:-(k-1)2≥0,
∴只有当k=1时,上式才能成立. …(10分)
又由(1)知k≤
| 1 |
| 4 |
∴不存在实数k使得x1•x2-x12-x22≥0成立. …(12分)
点评:本题考查一元二次方程的根的分布与系数的关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
已知函数f(x)=sin(
-x)(x∈R),下面结论错误的是( )
| π |
| 2 |
| A、函数f(x)的最小正周期为2π | ||
B、函数f(x)在区间,[0,
| ||
C、函数f(x)的图象关于点(
| ||
| D、函数f(x)是奇函数 |
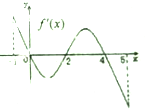 已知函数f(x)的定义域为[-1,5],部分对应值如下表.f(x)的导函数y=f′(x)的图象如图所示.下列关于函数f(x)的命题:①函数f(x)在[0,2]是减函数;②如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;③函数y=f(x)-a有4个零点时1<a<2.其中真命题的个数是( )
已知函数f(x)的定义域为[-1,5],部分对应值如下表.f(x)的导函数y=f′(x)的图象如图所示.下列关于函数f(x)的命题:①函数f(x)在[0,2]是减函数;②如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;③函数y=f(x)-a有4个零点时1<a<2.其中真命题的个数是( )