题目内容
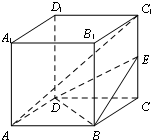 如图,在边长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点.
如图,在边长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点.(Ⅰ)证明:AC1∥平面BDE;
(Ⅱ)求三棱锥E-BCD的体积
(Ⅲ)求异面直线BC1,CD1所成角.
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(I)连接AC交BD于点O,连接EO.由三角形的中位线定理可得AC1∥EO.再利用线面平行的判定定理即可得出.
((III)连接BA1,A1C1.可得△A1BC1为等边三角形,四边形A1BCD1为平行四边形.于是A1B∥CD1,∠A1BC1为异面直线BC1,CD1所成角.
((III)连接BA1,A1C1.可得△A1BC1为等边三角形,四边形A1BCD1为平行四边形.于是A1B∥CD1,∠A1BC1为异面直线BC1,CD1所成角.
解答:
(I)证明:连接AC交BD于点O,连接EO.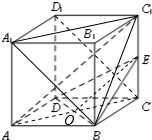
则AO=OC,又E是棱CC1的中点.
∴AC1∥EO.
∵EO?平面BDE,AC1?平面BDE,
∴AC1∥平面BDE;
(II)V三棱锥E-BCD=
S△BCD•EC=
×
×22×1=1.
(III)连接BA1,A1C1.
则△A1BC1为等边三角形,四边形A1BCD1为平行四边形.
∴A1B∥CD1,
∴∠A1BC1为异面直线BC1,CD1所成角.
∴∠A1BC1=60°为异面直线BC1,CD1所成角.

则AO=OC,又E是棱CC1的中点.
∴AC1∥EO.
∵EO?平面BDE,AC1?平面BDE,
∴AC1∥平面BDE;
(II)V三棱锥E-BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(III)连接BA1,A1C1.
则△A1BC1为等边三角形,四边形A1BCD1为平行四边形.
∴A1B∥CD1,
∴∠A1BC1为异面直线BC1,CD1所成角.
∴∠A1BC1=60°为异面直线BC1,CD1所成角.
点评:本题考查了正方体的性质、线面平行的判定定理、三角形的中位线定理、等边三角形的判定与性质、平行四边形的判定与性质定理、三棱锥的体积计算公式、异面直线所成的角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
在等差数列{an}中,a5+a13=40,则a8+a9+a10=( )
| A、72 | B、60 | C、48 | D、36 |
已知函数f(x)=sin(
-x)(x∈R),下面结论错误的是( )
| π |
| 2 |
| A、函数f(x)的最小正周期为2π | ||
B、函数f(x)在区间,[0,
| ||
C、函数f(x)的图象关于点(
| ||
| D、函数f(x)是奇函数 |