题目内容
已知{an}是等差数列,且满足am=n,an=m(m≠n),则am+n等于 .
考点:等差数列的性质
专题:等差数列与等比数列
分析:设出等差数列的首项和公差,直接由题意列方程组求解首项和公差,则第m+n项可求.
解答:
解:设等差数列的首项为a1,公差为d,由已知,
得
,解得
.
∴am+n=a1+(m+n-1)d=(m+n-1)-(m+n-1)=0.
故答案为:0.
得
|
|
∴am+n=a1+(m+n-1)d=(m+n-1)-(m+n-1)=0.
故答案为:0.
点评:本题考查了等差数列的通项公式,考查了方程组的解法,是基础的运算题.

练习册系列答案
相关题目
在等差数列{an}中,a5+a13=40,则a8+a9+a10=( )
| A、72 | B、60 | C、48 | D、36 |
下列集合中,只有一个子集的集合为( )
| A、{x|x2≤0} |
| B、{x|x3≤0} |
| C、{x|x2<0} |
| D、{x|x3<0} |
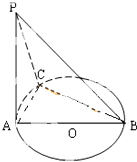 如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,AC=BC=4,PA=4
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,AC=BC=4,PA=4