题目内容
11.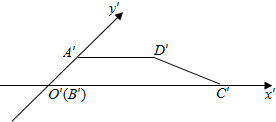 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是2$\sqrt{2}$.
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是2$\sqrt{2}$.
分析 由已知直角梯形ABCD中,AB⊥BC,AD=A′D′=2,BC=B′C′=4,AB=2A′B′=2,由此能求出直角梯形DC边的长度.
解答  解:由已知作出梯形ABCD是直角梯形,如右图:
解:由已知作出梯形ABCD是直角梯形,如右图:
∵按照斜二测画法画出它的直观图A′B′C′D′,A′D′=2,B′C′=4,A′B′=1,
∴直角梯形ABCD中,AB⊥BC,AD=A′D′=2,BC=B′C′=4,AB=2A′B′=2,
过D作DE⊥BC,交BC于E,则DE=AB=2,EC=BC-AD=4-2=2,
∴直角梯形DC边的长度为:$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查直角梯形中斜边长的求法,是基础题,解题时要认真审题,注意斜二测画法的合理运用.

练习册系列答案
相关题目
2.下列各数中最小的数为( )
| A. | 101111(2) | B. | 1210(3) | C. | 112(8) | D. | 69(12) |
6.一个圆锥的底面半径为2cm,高为6cm,在其中有一个高为3cm的内接圆柱,则圆柱的侧面积为( )
| A. | 2πcm2 | B. | 4πcm2 | C. | 6πcm2 | D. | 12πcm2 |
16.已知$|{\overrightarrow{AB}}|=|{\overrightarrow{AC}}|=2,\overrightarrow{AB}•\overrightarrow{AC}=2\sqrt{3}$,平面区域D由所有满足$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$(1≤λ≤a,1≤μ≤b)的点P构成,其面积为8,则4a+b的最小值为( )
| A. | 13 | B. | 12 | C. | $7\sqrt{2}$ | D. | $6\sqrt{2}$ |
 如图,点E在直角三角形ABC的斜边AB上,四边形CDEF为正方形,已知正方形CDEF的面积等于36.设∠CAB=θ,直角三角形ABC的周长L=12+$\frac{a(b+sinθ+cosθ)}{sinθcosθ}$.
如图,点E在直角三角形ABC的斜边AB上,四边形CDEF为正方形,已知正方形CDEF的面积等于36.设∠CAB=θ,直角三角形ABC的周长L=12+$\frac{a(b+sinθ+cosθ)}{sinθcosθ}$.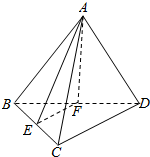 如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.
如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.