题目内容
化简：sin2α+sin2β+sin2αsin2β+cos2αcos2β= ．
考点：三角函数中的恒等变换应用
专题：计算题,三角函数的求值
分析：根据已知中只含有α与β正弦的平方和余弦的平方，我们可以使用同角三角函数关系中的平方关系解答本题，观察原式中的各项提取公因式后，易得结论
解答：
解：sin2α+sin2β+sin2αsin2β+cos2αcos2β
=sin2α（1+sin2β）+1-cos2β+cos2αcos2β
=sin2α（1+sin2β）+1+cos2β（cos2α-1）
=sin2α（1+sin2β）+1+（1-sin2β）（cos2α-1）
=sin2α（1+sin2β）+1-（1-sin2β）sin2α
=sin2α+sin2αsin2β+1-sin2α+sin2αsin2β
=2sin2αsin2β+1
故答案为：2sin2αsin2β+1
=sin2α（1+sin2β）+1-cos2β+cos2αcos2β
=sin2α（1+sin2β）+1+cos2β（cos2α-1）
=sin2α（1+sin2β）+1+（1-sin2β）（cos2α-1）
=sin2α（1+sin2β）+1-（1-sin2β）sin2α
=sin2α+sin2αsin2β+1-sin2α+sin2αsin2β
=2sin2αsin2β+1
故答案为：2sin2αsin2β+1
点评：本题考查的知识点是三角函数的恒等变换及化简求值，其中根据原式中角及三角函数名称以及式的形状，分析后选择适当的公式，是解答本题的关键，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
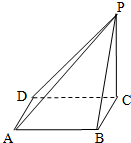如图，四棱锥P-ABCD的底面是正方形，PC⊥底面ABCD．
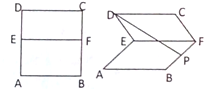已知E，F是正方形ABCD的边AD，BC中点，P是BF的中点，如图将该正方形以EF为棱折成60°的二面角D-EF-A，则直线DP和平面ABFE所成角的正切值是