题目内容
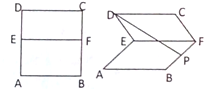 已知E,F是正方形ABCD的边AD,BC中点,P是BF的中点,如图将该正方形以EF为棱折成60°的二面角D-EF-A,则直线DP和平面ABFE所成角的正切值是
已知E,F是正方形ABCD的边AD,BC中点,P是BF的中点,如图将该正方形以EF为棱折成60°的二面角D-EF-A,则直线DP和平面ABFE所成角的正切值是考点:二面角的平面角及求法
专题:空间角
分析:设正方形ABCD的边长为a,过D作DO⊥平面ABFE,交AE于O,连结PO,则∠DOP是直线DP和平面ABFE所成角,由此能求出直线DP和平面ABFE所成角的正切值.
解答:
 解:设正方形ABCD的边长为a,过D作DO⊥平面ABFE,交AE于O,
解:设正方形ABCD的边长为a,过D作DO⊥平面ABFE,交AE于O,
连结PO,则∠DOP是直线DP和平面ABFE所成角,
∵E,F是正方形ABCD的边AD,BC中点,
P是BF的中点,将该正方形以EF为棱折成60°的二面角D-EF-A,
∴∠DEO=60°,DO=
=
a,PO=a,
∴tan∠DOP=
=
=
.
∴直线DP和平面ABFE所成角的正切值是
.
故答案为:
.
 解:设正方形ABCD的边长为a,过D作DO⊥平面ABFE,交AE于O,
解:设正方形ABCD的边长为a,过D作DO⊥平面ABFE,交AE于O,连结PO,则∠DOP是直线DP和平面ABFE所成角,
∵E,F是正方形ABCD的边AD,BC中点,
P是BF的中点,将该正方形以EF为棱折成60°的二面角D-EF-A,
∴∠DEO=60°,DO=
(
|
| ||
| 4 |
∴tan∠DOP=
| DO |
| PO |
| ||||
| a |
| ||
| 4 |
∴直线DP和平面ABFE所成角的正切值是
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查直线与平面所成角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为y=
x,它的一个焦点在抛物线y2=12x的准线上,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|