题目内容
设函数f（x）=g（x）+3，x∈[-t，t]（t＞0），其中g（x）是奇函数，若函数f（x）的最大值是M，最小值是m，则M+m的值为 ．
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：根据方程关系求出g（x）的最值，利用g（x）是奇函数的性质即可得到结论．
解答：
解：由f（x）=g（x）+3，x∈[-t，t]（t＞0），
得f（x）-3=g（x），x∈[-t，t]（t＞0），
则函数f（x）的最值和g（x）的最值同时取得，
∵函数f（x）的最大值是M，最小值是m，
∴函数g（x）的最大值是M-3，最小值是m-3，
∵g（x）是奇函数，
∴g（x）的最大值和最小值之和为0，
即M-3+m-3=0，
则M+m=6，
故答案为：6
得f（x）-3=g（x），x∈[-t，t]（t＞0），
则函数f（x）的最值和g（x）的最值同时取得，
∵函数f（x）的最大值是M，最小值是m，
∴函数g（x）的最大值是M-3，最小值是m-3，
∵g（x）是奇函数，
∴g（x）的最大值和最小值之和为0，
即M-3+m-3=0，
则M+m=6，
故答案为：6
点评：本题主要考查函数最值的求解，根据函数最值的性质以及奇函数最值的关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
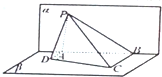如图所示，△PAB所在的平面α和四边形AB所在的平面β互相垂直，AD⊥α，bc⊥α，AD=4，BC=8，AB=6，若tan∠ADP-2tan∠BCP=1，则动点P在平面内α的轨迹是（ ）| A、椭圆的一部分 |
| B、线段 |
| C、双曲线的一部分 |
| D、以上都不是 |
若f（x）为偶函数，且x0是的y=f（x）+ex一个零点，则-x0一定是下列哪个函数的零点（ ）
| A、y=f（-x）ex-1 |
| B、y=f（x）ex+1 |
| C、y=f（x）ex-1 |
| D、y=f（x）e-x+1 |