题目内容
求函数f(x)=
+lg(4-x)的定义域.
| ||
| x-3 |
考点:对数函数的定义域
专题:函数的性质及应用
分析:根据开偶次方根被开方数大于等于0,分母不为0,对数函数的真数大于0,列出不等式求出定义域.
解答:
解:要使函数有意义,只需
解得2≤x<4且x≠3,
故函数f(x)=
+lg(4-x)的定义域为:{x|2≤x<4且x≠3}
|
解得2≤x<4且x≠3,
故函数f(x)=
| ||
| x-3 |
点评:本题考查求函数的定义域需注意:开偶次方根被开方数大于等于0,分母不为0,对数函数的真数大于0,底数大于0且不等于1.

练习册系列答案
相关题目
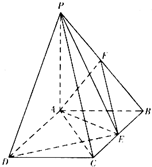 如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=
如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=