题目内容
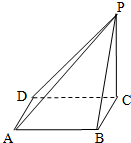如图，四棱锥P-ABCD的底面是正方形，PC⊥底面ABCD．（Ⅰ）若PC的中点为E，求证：PA∥平面BDE；
（Ⅱ）若E是直线PC上的动点，是否恒有BD⊥AE？证明你的结论．
考点：直线与平面垂直的性质,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）连结AC，设AC与BD交于O点，连结EO，易证EO为△PAC的中位线，从而OE∥PA，再利用线面平行的判断定理即可证得PA∥平面BDE；
（1）先证BD⊥平面PAC，又AE?平面PAC，从而得证．
（1）先证BD⊥平面PAC，又AE?平面PAC，从而得证．
解答：
证明：（1）连结AC，设AC与BD交于O点，连结EO．
∵底面ABCD是正方形，
∴O为AC的中点，又E为PC的中点
∴OE∥PA，
∵OE?平面BDE，PA?平面BDE，
∴PA∥平面BDE．…（6分）
（2）∵底面是正方形，
∴BD⊥AC，
又PC⊥底面ABCD，BD?面ABCD，
∴BD⊥PC，
又AC∩PC=C，AC?平面PAC，PC?平面PAC，
∴BD⊥平面PAC，
而E是直线PC上的动点，
∴AE?平面PAC，
∴BD⊥AE．
∵底面ABCD是正方形，
∴O为AC的中点，又E为PC的中点
∴OE∥PA，
∵OE?平面BDE，PA?平面BDE，
∴PA∥平面BDE．…（6分）
（2）∵底面是正方形，
∴BD⊥AC，
又PC⊥底面ABCD，BD?面ABCD，
∴BD⊥PC，
又AC∩PC=C，AC?平面PAC，PC?平面PAC，
∴BD⊥平面PAC，
而E是直线PC上的动点，
∴AE?平面PAC，
∴BD⊥AE．
点评：本题主要考查线面平行和线面垂直的相关内容．
练习册系列答案
通城学典默写能手系列答案
相关题目
已知点p（-1，-
）在角θ的终边上，且θ∈[0，2π），则θ的值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1（a＞0，b＞0）的一条渐近线方程为y=
x，它的一个焦点在抛物线y2=12x的准线上，则此双曲线的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知g（x）=1-2x，f[g（x）]=
，则f（-3）等于（ ）
| 1 |
| 2x+2 |
A、
| ||
B、
| ||
C、
| ||
| D、4 |