题目内容

空间给定不共面的A、B、C、D四个点，其中任意两点的距离都不相同，考虑具有如下性质的平面α：A、B、C、D中有三个点到α的距离相同，另外一个点到α的距离是前三个点到α的距离的2倍，这样的平面的个数是（　　）
A、15B、23C、26D、32
考点：平面与平面之间的位置关系
专题：空间位置关系与距离
分析：按照四个点的位置不同分类讨论．
解答： 解：首先取3个点相等，不相等的那个点有4种取法．
然后分3个点到平面α的距离相等，有以下2种可能性：
①全同侧，这样的平面有2个；
②不同侧，必然2个点在一侧，另1个点在一侧，1个点的取法有3种，并且平面过三角形两个点边上的中位线．考虑不相等的点与单侧点是否同侧有两种可能，每种情况下都唯一确定一个平面，有6个．
所以共有8个．
综上满足条件的这样的平面共有4×8=32个．
故选D．
点评：本题考查了空间点线面的关系，属于难题．
练习册系列答案
相关题目
两个袋中各装有编号为1，2，3，4，5的5个小球，分别从每个袋中摸出一个小球，所得两球编号数之和小于5的概率为
 
．
化简：sin2α+sin2β+sin2αsin2β+cos2αcos2β=
 
．
已知函数f（x）=x2+bx+c满足f（x+1）=x2+x+1，则b+c=
 
．
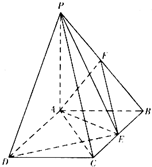如图，PA⊥平面ABCD，ABCD是矩形，PA=AB=
2
，AD=
3
，点F是PB的中点，点E是边BC上的动点．
（Ⅰ）求三棱锥E-PAD的体积；
（Ⅱ）当点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（Ⅲ）证明：无论点E在边BC的何处，都有PE⊥AF．
计算：
（1）16-0.75
（2）0.064 -
1
3

（3）（
1
4
） -
1
2
．
设函数f（x）=x2+|x-a|，g（x）=
a
x
．
（1）当a=0时，解关于x的不等式f（x）＞2；
（2）求函数f（x）的最小值；
（3）若?t∈（0，2），?x∈R使f（x）=g（t）成立，求实数a的取值范围．
下列命题正确的个数是（　　）
①梯形的四个顶点在同一平面内        
②三条平行直线必共面
③有三个公共点的两个平面必重合      
④每两条相交的且交点各不相同的四条直线一定共面．
A、1个B、2个C、3个D、4个
已知函数f（x）=2cosx（
3
sinx-cosx）+1（x∈R）
（1）求函数f（x）的最小正周期及在区间[0，
5π
12
]上的最大值和最小值；
（2）若f（x0）=
10
13
，x0∈[
π
2
，
7π
12
]，求cos2x0的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网