题目内容
求焦点在2x-6y-132=0上的抛物线标准方程及准线方程．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由已知条件，分别求出直线在x轴和y轴上的交点坐标，从而得到抛物线的焦点坐标，由此能求出抛物线方程．
解答：
解：在直线2x-6y-132=0中，
令x=0，得y=-22，
令y=0，得x=66．
∴抛物线的焦点坐标为F（0，-22）或F（66，0）．
当焦点F（66，0）时，
设抛物线的标准方程为y2=2px，p＞0，
则
=66，p=132，
∴抛物线的标准方程为：y2=264x，准线方程为：x=-132；
当焦点F（0，-22）时，
设抛物线的标准方程为x2=-2py，p＞0，
则
=22，p=44，
∴抛物线的标准方程为：x2=-88y，准线方程为：y=22．
令x=0，得y=-22，
令y=0，得x=66．
∴抛物线的焦点坐标为F（0，-22）或F（66，0）．
当焦点F（66，0）时，
设抛物线的标准方程为y2=2px，p＞0，
则
| p |
| 2 |
∴抛物线的标准方程为：y2=264x，准线方程为：x=-132；
当焦点F（0，-22）时，
设抛物线的标准方程为x2=-2py，p＞0，
则
| p |
| 2 |
∴抛物线的标准方程为：x2=-88y，准线方程为：y=22．
点评：本题考查抛物线的标准方程和准线方程的求法，是基础题，解题时要注意抛物线的标准方程的焦点坐标一定在坐标轴上．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
圆x2+y2+2y=1的半径为（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
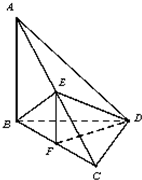如图，已知三棱锥A-BCD，AB⊥BD，AD⊥CD，E，F分别为AC，BC的中点，且△BEC为正三角形．