题目内容
双曲线
-
=1(m>0)的渐近线与圆x2+(y-2)2=1相切,则实数m的值为( )
| x2 |
| m2 |
| y2 |
| m2+1 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
考点:圆与圆锥曲线的综合,直线与圆的位置关系,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出双曲线的渐近线方程,然后利用圆的圆心到直线的距离等于半径,即可求出m的值即可.
解答:
解:双曲线
-
=1(m>0)的渐近线之一为:y=
x,
圆x2+(y-2)2=1的圆心(0,2)半径为1,
双曲线
-
=1(m>0)的渐近线与圆x2+(y-2)2=1相切,
可得
=1,解得m=
.
故选:B.
| x2 |
| m2 |
| y2 |
| m2+1 |
| ||
| m |
圆x2+(y-2)2=1的圆心(0,2)半径为1,
双曲线
| x2 |
| m2 |
| y2 |
| m2+1 |
可得
| |2m| | ||
|
| ||
| 2 |
故选:B.
点评:本题考查双曲线与圆的位置关系,双曲线的简单性质,点到直线的距离公式的应用,考查计算能力.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
如果两个球的体积之比为8:27,那么两个球的表面积之比为( )
| A、2:3 | B、2:9 |
| C、4:9 | D、8:27 |
函数f(x)=
的图象大致为( )
|
A、 |
B、 |
C、 |
D、 |
下列四个数中最小者是( )
A、log3
| ||
| B、log32 | ||
| C、log23 | ||
| D、log3(log23) |
若数列{an}满足a1=1,a2=2,anan-2=an-1(n≥3),则a2014的值为( )
| A、2 | ||
B、
| ||
| C、1 | ||
| D、22014 |
 已知函数f(x)=2sinxcos(x-φ)-
已知函数f(x)=2sinxcos(x-φ)-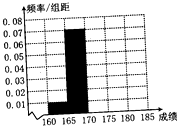 某校在自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布图的一部分(每一组均包括左端点数据),且第三组、第四组、第五组的频数之比一次为3:2:1.
某校在自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布图的一部分(每一组均包括左端点数据),且第三组、第四组、第五组的频数之比一次为3:2:1.