题目内容
如果两个球的体积之比为8:27,那么两个球的表面积之比为( )
| A、2:3 | B、2:9 |
| C、4:9 | D、8:27 |
考点:球的体积和表面积
专题:空间位置关系与距离
分析:通过体积比等于相似比的立方,求出两个球的半径的比,表面积之比等于相似比的平方,即可求出结论.
解答:
解:两个球的体积之比为8:27,根据体积比等于相似比的立方,表面积之比等于相似比的平方,
可知两球的半径比为2:3,
从而这两个球的表面积之比为4:9.
故选:C.
可知两球的半径比为2:3,
从而这两个球的表面积之比为4:9.
故选:C.
点评:本题是基础题,考查相似比的知识,考查计算能力,常考题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
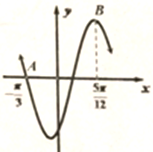 函数f(x)=2sin(ωx+φ)(ω>0,-
函数f(x)=2sin(ωx+φ)(ω>0,-| π |
| 2 |
| π |
| 2 |
A、2,-
| ||
B、2,-
| ||
C、4,-
| ||
D、4,
|
已知函数f(x)=asinx+bcosx(x∈R),若x=x0是函数f(x)的一条对称轴,且tanx0=2,则点(a,b)所在的直线为( )
| A、x-2y=0 |
| B、x+2y=0 |
| C、2x-y=0 |
| D、2x+y=0 |
双曲线
-
=1(m>0)的渐近线与圆x2+(y-2)2=1相切,则实数m的值为( )
| x2 |
| m2 |
| y2 |
| m2+1 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
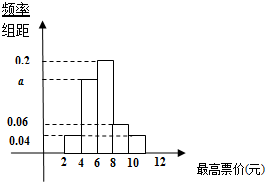 2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:
2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下: