题目内容
已知sinα=
,且α是第一象限角
(Ⅰ)求cosα的值
(Ⅱ)求tan(π+α)cos(π-α)-sin(
+α)的值.
| ||
| 5 |
(Ⅰ)求cosα的值
(Ⅱ)求tan(π+α)cos(π-α)-sin(
| π |
| 2 |
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(Ⅰ)利用同角三角函数的基本关系式直接求cosα的值
(Ⅱ)通过弦切互化以及诱导公式直接求tan(π+α)cos(π-α)-sin(
+α)的值即可.
(Ⅱ)通过弦切互化以及诱导公式直接求tan(π+α)cos(π-α)-sin(
| π |
| 2 |
解答:
解:(Ⅰ)sinα=
,且α是第一象限角
cosα=
=
(Ⅱ)tanαcos(π-α)-sin(
+α)=-tanαcosα-cosα=-sinα-cosα=-
-
=-
.
| ||
| 5 |
cosα=
| 1-sin2α |
2
| ||
| 5 |
(Ⅱ)tanαcos(π-α)-sin(
| π |
| 2 |
| ||
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |
点评:本题考查诱导公式的应用,同角三角函数的基本关系式,考查计算能力.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
双曲线
-
=1(m>0)的渐近线与圆x2+(y-2)2=1相切,则实数m的值为( )
| x2 |
| m2 |
| y2 |
| m2+1 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
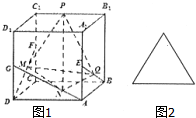 如图1,已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1ClD1的棱AA1、CC1、DD1的中点,点M、N、Q、P分别在线段DF、AG、BE、C1B1上运动,当以M、N、Q、P为顶点的三棱锥P-MNQ的俯视图是如图2所示的等腰三角形时,点P到平面MNQ的距离为( )
如图1,已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1ClD1的棱AA1、CC1、DD1的中点,点M、N、Q、P分别在线段DF、AG、BE、C1B1上运动,当以M、N、Q、P为顶点的三棱锥P-MNQ的俯视图是如图2所示的等腰三角形时,点P到平面MNQ的距离为( )A、
| ||
B、
| ||
C、
| ||
| D、a |
若α的终边与单位圆交于点(
,-
),则cosα=( )
| 1 |
| 2 |
| ||
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若集合A={x|-2<x<1},B={x|0<x<1},则集合A∩B=( )
| A、{x|-1<x<1} |
| B、{x|-2<x<1} |
| C、{x|-2<x<2} |
| D、{x|0<x<1} |