题目内容
若数列{an}满足a1=1,a2=2,anan-2=an-1(n≥3),则a2014的值为( )
| A、2 | ||
B、
| ||
| C、1 | ||
| D、22014 |
考点:数列递推式
专题:等差数列与等比数列
分析:首先根据递推关系式,求出一部分的值,在观察出数列的各项具备的规律,利用周期最后求出结果.
解答:
解:数列{an}满足:a1=1,a2=2,
利用anan-2=an-1(n≥3且n∈N),
则:a3=2,a4=
=1,a5=
=
,a6=
=
,a7=
=1,a8=
=2,…
1,2,2,1,
,
,1,2,2,1,
,
,1,2,…
所以:数列的周期为:6
2014=335×6+4
所以:a2014=a4=1
故选:C.
利用anan-2=an-1(n≥3且n∈N),
则:a3=2,a4=
| a3 |
| a2 |
| a4 |
| a3 |
| 1 |
| 2 |
| a5 |
| a4 |
| 1 |
| 2 |
| a6 |
| a5 |
| a7 |
| a6 |
1,2,2,1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以:数列的周期为:6
2014=335×6+4
所以:a2014=a4=1
故选:C.
点评:本题考查的知识要点:数列递推关系式的应用,数列的周期性在运算中的应用.属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
双曲线
-
=1(m>0)的渐近线与圆x2+(y-2)2=1相切,则实数m的值为( )
| x2 |
| m2 |
| y2 |
| m2+1 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
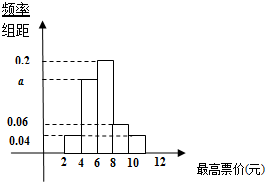 2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:
2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下: