题目内容
若曲线C1:y=x2与曲线C2:y=aex(a>0)存在公切线,则a的取值范围为( )
A、[
| ||
B、(0,
| ||
C、[
| ||
D、(0,
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:分别求出两个函数的导函数,由两函数在切点处的导数相等,并由斜率公式,得到由此得到m=2n-2,则4n-4=aen有解.再由导数即可进一步求得a的取值.
解答:
解:y=x2在点(m,m2)的切线斜率为2m,
y=aex在点(n,aen)的切线斜率为aen,
如果两个曲线存在公共切线,那么:2m=aen.
又由斜率公式得到,2m=
,
由此得到m=2n-2,
则4n-4=aen有解.
由y=4x-4,y=aex的图象有交点即可.
设切点为(s,t),则aes=4,且t=4s-4=aes,
即有切点(2,4),a=
,
故a的取值范围是:0<a≤
,
故选D.
y=aex在点(n,aen)的切线斜率为aen,
如果两个曲线存在公共切线,那么:2m=aen.
又由斜率公式得到,2m=
| m2-aen |
| m-n |
由此得到m=2n-2,
则4n-4=aen有解.
由y=4x-4,y=aex的图象有交点即可.
设切点为(s,t),则aes=4,且t=4s-4=aes,
即有切点(2,4),a=
| 4 |
| e2 |
故a的取值范围是:0<a≤
| 4 |
| e2 |
故选D.
点评:本题考查利用导数研究曲线上某点的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
如图程序框图中,若输出S=
+
,则p的值为( )
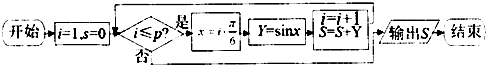
| 3 |
| 2 |
| 3 |
| A、3 | B、4 | C、5 | D、6 |
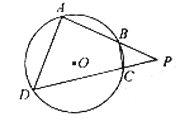 如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若PB=1,PD=3,则
如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若PB=1,PD=3,则