Question

正四棱锥P-ABCD的底面边长是2，侧棱长是

6

，且它的五个顶点都在同一个球面上，则此球的半径是

 

．

Answer 1

考点：球内接多面体

专题：计算题,空间位置关系与距离

分析：设球半径为R，底面中心为O'且球心为O．正四棱锥P-ABCD中根据AB=2且PA=

6

，算出AO'=

2

、PO'=2、OO'=2-R，在Rt△AOO′中利用勾股定理建立关于R的等式，解出R=

3

2

，再利用球的体积公式即可得到外接球的体积．

解答： 解：如图所示，设球半径为R，底面中心为O'且球心为O，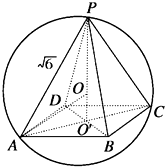
∵正四棱锥P-ABCD中AB=2，PA=

6

，
∴AO'=

2

2

AB=

2

，可得PO'=

PA2-AO′2

=2，OO'=PO'-PO=2-R．
∵在Rt△AOO'中，AO²=AO'²+OO'²，
∴R²=（

2

）²+（2-R）²，解之得R=

3

2

，
因此可得外接球的体积V=

4

3

πR³=

4

3

π•(

3

2

)3=

9

2

π．
故答案为：

9

2

π．

点评：本题给出正四棱锥的形状，求它的外接球的体积，着重考查了正棱锥的性质、多面体的外接球、勾股定理与球的体积公式等知识，属于中档题．