题目内容
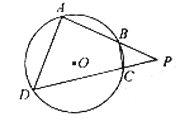如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P．若PB=1，PD=3，则| BC |
| AD |
考点：与圆有关的比例线段
专题：立体几何
分析：由切割线定理，得到PB×PA=PC×PD，由圆的内接四边形的性质得△PBC∽△PDA，由此能求出
=
=
．
| PB |
| PD |
| BC |
| AD |
| 1 |
| 3 |
解答：
解：由切割线定理，得到PB×PA=PC×PD
∵PB=1，PD=3
∠A=∠PCB，∠D=∠PBC
∴△PBC∽△PDA
∴
=
=
．
故答案为：
．
∵PB=1，PD=3
∠A=∠PCB，∠D=∠PBC
∴△PBC∽△PDA
∴
| PB |
| PD |
| BC |
| AD |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查线段的比值的求法，是基础题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
相关题目
若曲线C1：y=x2与曲线C2：y=aex（a＞0）存在公切线，则a的取值范围为（ ）
A、[
| ||
B、（0，
| ||
C、[
| ||
D、（0，
|
已知函数f（x）=a（x-
）-2lnx（a∈R）．
（1）求函数f（x）的单调区间；
（2）设函数g（x）=-
．若至少存在一个x0∈[1，4]，使得f（x0）=g（x0）成立，求实数a的取值范围．
| 1 |
| x |
（1）求函数f（x）的单调区间；
（2）设函数g（x）=-
| a |
| x |
如图（1）、（2），它们都表示的是输出所有立方小于729的正整数的程序框图，那么判断框中应分别补充的条件为（ ）
| A、（1）n3≥729？（2）n3＜729？ |
| B、（1）n3≤729？（2）n3＞729？ |
| C、（1）n3＜729？（2）n3≥729？ |
| D、（1）n3＜729？（2）n3＜729？ |