题目内容
设f（x）为定义在R上的奇函数，当x≥0时，f（x）=2x+3log2（x+1）+m（m为常数），则f（-1）= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据奇函数的性质，先根据f（0）=0求出m的值，然后利用f（-1）=-f（1）求出f（-1）的值．
解答：
解：因为该函数为奇函数，且在x=0时有意义，
所以f（0）=1+m=0，所以m=-1．
所以x≥0时，f（x）=2x+3log2（x+1）-1．
所以f（-1）=-f（1）=-（21+3log22-1）=-4．
故答案为：-4．
所以f（0）=1+m=0，所以m=-1．
所以x≥0时，f（x）=2x+3log2（x+1）-1．
所以f（-1）=-f（1）=-（21+3log22-1）=-4．
故答案为：-4．
点评：本题考查了奇函数的性质，以及利用奇函数的性质求函数值的问题．属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
若某个几何体的三视图（单位：cm）如图所示，则该几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
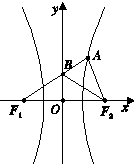如图，双曲线C：| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、1+
| ||||
C、
| ||||
D、
|
已知双曲线x2-
=1（b＞0）的一条渐近线的方程为y=2x，则b的值等于（ ）
| y2 |
| b2 |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |