题目内容
已知向量
=(3,4),
=(2,x),如果向量
与
垂直,则x的值为 .
| a |
| b |
| a |
| b |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:由垂直关系可得
•
=3×2+4x=0,解方程可得.
| a |
| b |
解答:
解:∵向量
=(3,4),
=(2,x),且
与
垂直,
∴
•
=3×2+4x=0,解得x=-
故答案为:-
| a |
| b |
| a |
| b |
∴
| a |
| b |
| 3 |
| 2 |
故答案为:-
| 3 |
| 2 |
点评:本题考查平面向量的数量积和垂直关系,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在锐角△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,其中B=
,b=
,则边长c的取值范围是( )
| π |
| 4 |
| 2 |
A、(1,
| ||
B、(
| ||
| C、(1,2) | ||
D、[
|
已知为虚数单位,复数z=i(2-i),则|z|=( )
A、
| ||
B、
| ||
| C、1 | ||
| D、3 |
在△ABC中,
=1,
=-2,则AB边的长度为( )
| ||||
I
|
| ||||
I
|
| A、1 | B、3 | C、5 | D、9 |
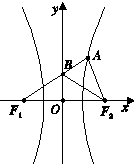 如图,双曲线C:
如图,双曲线C: