题目内容
在平行四边形ABCD中,AC为一条对角线,
=(2,4),
=(1,3),则
等于( )
| AB |
| AC |
| BD |
| A、(2,4) |
| B、(3,5) |
| C、(-3,-5) |
| D、(-2,-4) |
考点:平面向量的坐标运算
专题:平面向量及应用
分析:利用平行四边形对边平行相等,结合向量的运算法则,求解即可.
解答:
解:∵
=
=
-
,
∴
=
-
=
-2
=(-3,-5).
故选:C.
| AD |
| BC |
| AC |
| AB |
∴
| BD |
| AD |
| AB |
| AC |
| AB |
故选:C.
点评:本题考查向量的基本运算,向量的坐标求法,考查计算能力.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
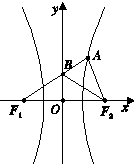 如图,双曲线C:
如图,双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、1+
| ||||
C、
| ||||
D、
|
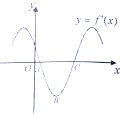 函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,A,C为图象与x轴的两个交点,B为图象的最低点,若在曲线
函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,A,C为图象与x轴的两个交点,B为图象的最低点,若在曲线 |
| ABC |
数列{an}中,已知a1=1,对任意的k∈N*,有a2k-1,a2k,a2k+1成等比数列,且公比为2k,则a101的值为( )
| A、2 502 |
| B、250×51 |
| C、2 512 |
| D、2101×102 |
若函数y=2x图象上存在点(x,y)满足约束条件
,则实数m的最大值为( )
|
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
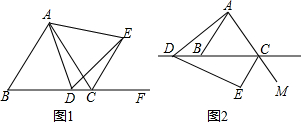 如图1所示,点D是等边三角形ABC的边BC上一点,连结AD作∠ADE=60°,交∠ABC的外角平分线CE于E
如图1所示,点D是等边三角形ABC的边BC上一点,连结AD作∠ADE=60°,交∠ABC的外角平分线CE于E