题目内容
已知椭圆方程为
+
=1，焦点在x轴上，则其焦距等于（ ）
| x2 |
| 8 |
| y2 |
| m2 |
A、2
| ||||
B、2
| ||||
C、2
| ||||
D、2
|
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：利用椭圆的简单性质直接求解．
解答：
解：∵椭圆方程为
+
=1，焦点在x轴上，
∴c=
，
∴该椭圆方程的焦距为2
．
故选：A．
| x2 |
| 8 |
| y2 |
| m2 |
∴c=
| 8-m2 |
∴该椭圆方程的焦距为2
| 8-m2 |
故选：A．
点评：本题考查椭圆的焦距的求法，是基础题，解题时要认真审题，注意椭圆的简单性质的灵活运用．
练习册系列答案
相关题目
已知实数x，y满足x+4y=1，则xy的值域为（ ）
A、（0，
| ||||
B、[-
| ||||
C、（-∞，
| ||||
D、（-∞，
|
若Sn=cos
+cos
+…+cos
（n∈N*），则在S1，S2，…，S2014中，正数的个数是（ ）
| π |
| 8 |
| 2π |
| 8 |
| nπ |
| 8 |
| A、882 | B、756 |
| C、750 | D、378 |
直线3x-y+1=0的斜率是（ ）
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
已知一几何体三视图如图，则其体积为（ ）
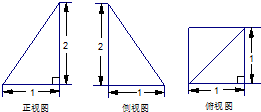
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
设a，b∈R，则“a
+b
=1”是“a2+b2=1”的（ ）
| 1-b2 |
| 1-a2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
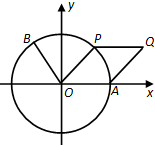如图，点A是单位圆与x轴正半轴的交点，点B（-