题目内容

求下列函数的导函数
（1）y=xtanx-
2
sinx

（2）y=
lnx
x+1
-2x．
考点：导数的运算
专题：导数的概念及应用,导数的综合应用
分析：根据函数的导数公式进行求导即可得到结论．
解答： 解：（1）∵y=xtanx-
2
sinx
=
xsinx
cosx
-
2
sinx
，
∴y′=
(xsinx)′cosx-xsinx(cosx)′
cos2x
-
-2cosx
sin2x

=
(sinx+xcosx)cosx+xsinxcosx
cos2x
+
2cosx
sin2x

=
(x+1)sinxcosx+xcos2x
cos2x
+
2cosx
sin2x
．
（2）∵y=
lnx
x+1
-2x，
∴y′=
1
x
•(x+1)-lnx
(x+1)2
-2xln2
=
x+1-xlnx
x(x+1)2
-2xln2．
点评：本题主要考查导数的基本运算，要求熟练掌握常见函数的导数公式和导数的运算法则．
练习册系列答案
相关题目
已知向量
a
=（x1，y1），
b
=（x2，y2），
e
=（1，0），若
a
≠
b
，|
a
-
b
|=2，且
a
-
b
与
e
的夹角为
π
3
，则x1-x2=（　　）
A、2
B、±
3
C、±
2
D、1
为了调查大学生对吸烟是否影响学习的看法，询问了大学一、二年级的200个大学生，询问的结果记录如下：其中大学一年级110名学生中有45人认为不会影响学习，有65人认为会影响学习，大学二年级90名学生中有55人认为不会影响学习，有35人认为会影响学习；
（1）根据以上数据绘制一个2×2的列联表；
（2）据此回答，能否有99%的把握断定大学生因年级不同对吸烟问题所持态度也不同？
附表：
p（K2≥k0） 0.05 0.025 0.010 0.005 0.001
k0 3.841 5.024 6.635 7.789 10.828
判断并证明函数f（x）=
2x-1
+x的单调性．
袋子A和B中装有若干个均匀的红球和白球，从A中摸出一个红球的概率是
1
3
，从B中摸出一个红球的概率为p．
（Ⅰ）从A中有放回地摸球，每次摸出一个，共摸5次．求恰好有2次摸到红球但不连续的概率；   
（Ⅱ）若A、B两个袋子中的球数之比为1：2，将A、B中的球装在一起后，从中摸出一个红球的概率是
2
5
，求p的值．
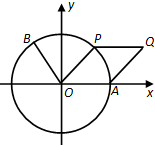如图，点A是单位圆与x轴正半轴的交点，点B（-
3
5
，
4
5
），∠AOB=α，
π
2
＜α＜π，|
OP
|=1，∠AOP=θ，0＜θ＜
π
2
．
（1）若cos（α-θ）=-
16
65
，求点P的坐标；
（2）若四边形OAQP为平行四边形且面积为S，求S+
OA
•
OQ
的最大值．
已知角α的终边经过点P（1，
3
）
（1）求sin（π-α）-sin（
π
2
+α）的值；       
（2）写出角α的集合S．
已知sinθ=
m-3
m+5
，cosθ=
4-2m
m+5
，则m等于
 
．
(2
x
-
1
x
)6的展开式中的常数项等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网