题目内容
已知f(x+
)=
,则f(x)= .
| 1 |
| x |
| x2+x+1 |
| x2 |
考点:函数解析式的求解及常用方法
专题:换元法
分析:用换元法求函数的解析式,令t=x+
,解出x,代入解析式中.
| 1 |
| x |
解答:
解:令t=x+
,则x2-tx+1=0,得x1=
,x2=
,
当x=x1时,f(t)=1+
+
=1+
+(
)2=
,
当x=x2时,f(t)=1+
+
=1+
+(
)2=
,
∴f(x)=
,f(x)=
.
故答案为:f(x)=
,f(x)=
.
| 1 |
| x |
t+
| ||
| 2 |
t-
| ||
| 2 |
当x=x1时,f(t)=1+
| 1 |
| x |
| 1 |
| x2 |
| 2 | ||
t+
|
| 2 | ||
t+
|
(t+1)(t-
| ||
| 2 |
当x=x2时,f(t)=1+
| 1 |
| x |
| 1 |
| x2 |
| 2 | ||
t-
|
| 2 | ||
t-
|
(t+1)(t+
| ||
| 2 |
∴f(x)=
(t+1)(t-
| ||
| 2 |
(t+1)(t+
| ||
| 2 |
故答案为:f(x)=
(x+1)(x-
| ||
| 2 |
(x+1)(x+
| ||
| 2 |
点评:本题换元时,用t表示x,有两个值,要分别带入,考查了换元法.属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
按照如图的程序运行,则输出的K值为( )


| A、2 | B、3 | C、4 | D、5 |
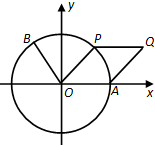 如图,点A是单位圆与x轴正半轴的交点,点B(-
如图,点A是单位圆与x轴正半轴的交点,点B(-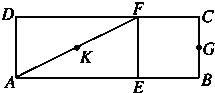 如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为
如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为