题目内容
已知函数(x-1)f(
)-f(x)=x,其中x≠1,求函数f(x)的解析式.
| x+1 |
| x-1 |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:首先,令
=t,解得x=
,然后,将此代人已知等式,化简得到
f(t)-f(
)=
,然后,联立方程组,从而得到函数f(x)的解析式.
| x+1 |
| x-1 |
| t+1 |
| t-1 |
| 2 |
| t-1 |
| t+1 |
| t-1 |
| t+1 |
| t-1 |
解答:
解:设
=t,
则x=
,
∴(
-1)f(t)-f(
)=
,
∴
f(t)-f(
)=
∴
f(x)-f(
)=
①
∵(x-1)f(
)-f(x)=x ②
联立①②,解得
f(x)=2x+1,(x≠1),
∴函数f(x)的解析式f(x)=2x+1,(x≠1).
| x+1 |
| x-1 |
则x=
| t+1 |
| t-1 |
∴(
| t+1 |
| t-1 |
| t+1 |
| t-1 |
| t+1 |
| t-1 |
∴
| 2 |
| t-1 |
| t+1 |
| t-1 |
| t+1 |
| t-1 |
∴
| 2 |
| x-1 |
| x+1 |
| x-1 |
| x+1 |
| x-1 |
∵(x-1)f(
| x+1 |
| x-1 |
联立①②,解得
f(x)=2x+1,(x≠1),
∴函数f(x)的解析式f(x)=2x+1,(x≠1).
点评:本题重点考查函数的解析式求解方法,理解换元法在求解函数解析式中的应用,属于中档题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
设a,b∈R,则“a
+b
=1”是“a2+b2=1”的( )
| 1-b2 |
| 1-a2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
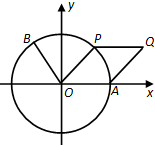 如图,点A是单位圆与x轴正半轴的交点,点B(-
如图,点A是单位圆与x轴正半轴的交点,点B(-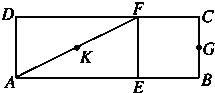 如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为
如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为