题目内容
益阳市箴言中学学校团委为三个年级提供了“甲、乙、丙、丁”学雷锋的四个不同活动内容,每个年级任选其中一个.求:
(1)三个年级选择3个不同活动内容的概率;
(2)恰有2个活动内容被选择的概率;
(3)选择甲活动内容的年级个数ξ的分布列.
(1)三个年级选择3个不同活动内容的概率;
(2)恰有2个活动内容被选择的概率;
(3)选择甲活动内容的年级个数ξ的分布列.
考点:离散型随机变量的期望与方差
专题:综合题,概率与统计
分析:(1)每个年级任选其中一个,都有4种选择方法,三个年级共有43种选择方法,其中三个年级选择3个不同活动内容,共有
种选择方法,可求三个年级选择3个不同活动内容的概率;
(2)恰有2个活动内容被选择,共有
(23-2)=36种选择方法,可得恰有2个活动内容被选择的概率;
(3)ξ的取值为0,1,2,3,求出相应的概率,即可确定选择甲活动内容的年级个数ξ的分布列.
| A | 3 4 |
(2)恰有2个活动内容被选择,共有
| C | 2 4 |
(3)ξ的取值为0,1,2,3,求出相应的概率,即可确定选择甲活动内容的年级个数ξ的分布列.
解答:
解:(1)每个年级任选其中一个,都有4种选择方法,三个年级共有43种选择方法,其中三个年级选择3个不同活动内容,共有
种选择方法,所以三个年级选择3个不同活动内容的概率为
=
;
(2)恰有2个活动内容被选择,共有
(23-2)=36种选择方法,所以恰有2个活动内容被选择的概率为
=
;
(3)ξ的取值为0,1,2,3,则
P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=3)=
=
.
ξ的分布列为
| A | 3 4 |
| ||
| 43 |
| 3 |
| 8 |
(2)恰有2个活动内容被选择,共有
| C | 2 4 |
| 36 |
| 43 |
| 9 |
| 16 |
(3)ξ的取值为0,1,2,3,则
P(ξ=0)=
| 33 |
| 43 |
| 27 |
| 64 |
| 3•32 |
| 43 |
| 27 |
| 64 |
| ||||
| 43 |
| 9 |
| 64 |
| 1 |
| 43 |
| 1 |
| 64 |
ξ的分布列为
ξ |
0 | 1 | 2 | 3 | ||||||||
P |
|
|
|
|
点评:本题考查概率的计算,考查分布列,正确计算概率是关键.

练习册系列答案
相关题目
若Sn=cos
+cos
+…+cos
(n∈N*),则在S1,S2,…,S2014中,正数的个数是( )
| π |
| 8 |
| 2π |
| 8 |
| nπ |
| 8 |
| A、882 | B、756 |
| C、750 | D、378 |
设a,b∈R,则“a
+b
=1”是“a2+b2=1”的( )
| 1-b2 |
| 1-a2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
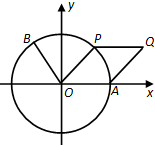 如图,点A是单位圆与x轴正半轴的交点,点B(-
如图,点A是单位圆与x轴正半轴的交点,点B(-