题目内容
18.已知等差数列{an}的前n项和为Sn,若a3=9-a6,则S8=36.分析 可得a1+a8=9,代入求和公式计算可得.
解答 解:由题意可得a3+a6=9,
由等差数列的性质可得a1+a8=9
故S8=$\frac{8}{2}$(a1+a8)=4×9=36
故答案为:36.
点评 本题考查等差数列的求和公式和性质,属基础题.

练习册系列答案
相关题目
8.如果$\frac{x^2}{1-2k}-\frac{y^2}{k-2}=1$表示焦点在y轴上的双曲线,那么实数k的取值范围是( )
| A. | $({\frac{1}{2},2})$ | B. | $({\frac{1}{2},1})∪({1,2})$ | C. | (1,2) | D. | $({\frac{1}{2},∞})$ |
6.设α,β是两个平面,l,m是两条直线,下列各条件,可以判断α∥β的有( )
①l?α,m?α,且l∥β,m∥β,②l?α,m?β,且l∥β,m∥α,③l∥α,m∥β,且l∥m,④l∥α,l∥β,m∥α,m∥β,且l,m互为异面直线.
①l?α,m?α,且l∥β,m∥β,②l?α,m?β,且l∥β,m∥α,③l∥α,m∥β,且l∥m,④l∥α,l∥β,m∥α,m∥β,且l,m互为异面直线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点且垂直于x轴的直线与双曲线交于A,B两点,与双曲线的渐近线交于C,D两点,若|AB|≥$\frac{5}{13}$|CD|,则该双曲线的离心率的取值范围为( )
| A. | [$\frac{14}{13}$,+∞) | B. | [$\frac{13}{12}$,+∞) | C. | [$\frac{15}{13}$,2) | D. | [$\frac{5}{4}$,2) |
8.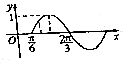 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )
 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
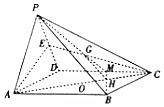 如图,P是平行四边形ABCD所在平面外一点,E是PD的中点.
如图,P是平行四边形ABCD所在平面外一点,E是PD的中点.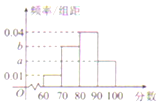 某校高三年级的一次测验成绩的频率分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取100人了解情况,已知70~80分数段抽取了30人,则全体高三年级学生的平均分数为82(以各组区间的中点值代表改组的取值)
某校高三年级的一次测验成绩的频率分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取100人了解情况,已知70~80分数段抽取了30人,则全体高三年级学生的平均分数为82(以各组区间的中点值代表改组的取值)