题目内容
8.如果$\frac{x^2}{1-2k}-\frac{y^2}{k-2}=1$表示焦点在y轴上的双曲线,那么实数k的取值范围是( )| A. | $({\frac{1}{2},2})$ | B. | $({\frac{1}{2},1})∪({1,2})$ | C. | (1,2) | D. | $({\frac{1}{2},∞})$ |
分析 根据题意,由双曲线的标准方程可得$\left\{\begin{array}{l}{1-2k<0}\\{k-2<0}\end{array}\right.$,解可得k的范围,即可得答案.
解答 解:根据题意,如果$\frac{x^2}{1-2k}-\frac{y^2}{k-2}=1$表示焦点在y轴上的双曲线,
则有$\left\{\begin{array}{l}{1-2k<0}\\{k-2<0}\end{array}\right.$,
解可得$\frac{1}{2}$<k<2,
即k的取值范围是($\frac{1}{2}$,2);
故选:A.
点评 本题考查双曲线的标准方程,关键是熟悉掌握焦点在y轴上的双曲线的形式.

练习册系列答案
相关题目
19.下列函数中只有一个零点的是( )
| A. | y=x-1 | B. | y=x2-1 | C. | y=2x | D. | y=lgx |
16.若满足条件C=60°,AB=$\sqrt{3}$的△ABC有两个,那么BC的取值范围是( )
| A. | $(1,\sqrt{2})$ | B. | (1,2) | C. | $(\sqrt{2},\sqrt{3})$ | D. | $(\sqrt{3},2)$ |
3.已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC.若B=90°,且$a=\sqrt{3}$,则△ABC的面积为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 3 |
17.执行如图所示的程序框图,若输入n=10,则输出的s值为( )
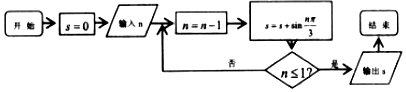

| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |