题目内容
8.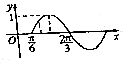 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,再根据正弦函数图象的对称性,求得 x1+x2=$\frac{5π}{6}$,可得f(x1+x2)的值.
解答 解:由函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象,
可得$\frac{1}{2}•\frac{2π}{ω}=\frac{2π}{3}-\frac{π}{6}$,∴ω=2.
再根据五点法作图可的2•$\frac{π}{6}$+φ=0,∴φ=-$\frac{π}{3}$,f(x)=sin(2x-$\frac{π}{3}$).
x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
则$\frac{1}{2}$(x1+x2)=$\frac{5π}{12}$,
∴x1+x2=$\frac{5π}{6}$,f(x1+x2)=sin(2•$\frac{5π}{6}$-$\frac{π}{3}$)=-$\frac{\sqrt{3}}{2}$,
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
17.执行如图所示的程序框图,若输入n=10,则输出的s值为( )
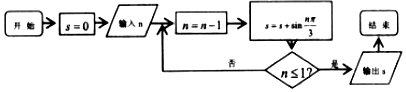

| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
3.函数f(x)=-|x-1|,g(x)=x2-2x,定义$F(x)=\left\{\begin{array}{l}f(x),f(x)≥g(x)\\ g(x),f(x)<g(x)\end{array}\right.$,则F(x)满足( )
| A. | 既有最大值,又有最小值 | B. | 只有最小值,没有最大值 | ||
| C. | 只有最大值,没有最小值 | D. | 既无最大值,也无最小值 |
17.11、设函数f(x)是奇函数,f(-2)=0,当x>0时,xf'(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(2,+∞) | C. | (-∞,-2)∪(-2,0) | D. | (0,2)∪(2,+∞) |
18.从狼堡去青青草原的道路有6条,从青青草原去羊村的道路有20条,狼堡与羊村被青青草原隔开,则狼去羊村的不同走法有( )
| A. | 120 | B. | 26 | C. | 20 | D. | 6 |
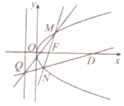 已知抛物线ω:y2=ax(a>0)上一点,P(t,2)到焦点F的距离为2t
已知抛物线ω:y2=ax(a>0)上一点,P(t,2)到焦点F的距离为2t