题目内容
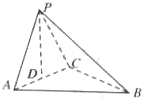 如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4
如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4| 5 |
(Ⅰ)证明:平面PBC⊥平面PAC;
(Ⅱ)若PD=2
| 3 |
考点:用空间向量求平面间的夹角,平面与平面垂直的判定,二面角的平面角及求法
专题:空间角
分析:(Ⅰ)要证平面PBC⊥平面PAC,可以证明平面PBC经过平面PAC的一条垂线BC,由已知点P在平面ABC上的射影D可知PD⊥BC,再通过三角形的边的关系得到AC⊥BC.然后由线面垂直的判定定理得到证明;
(Ⅱ)以C为坐标原点建立如图所示空间直角坐标系,由二面角A-PB-C的两个面的法向量所成角的余弦值求得二面角A-PB-C的平面角的余弦值.
(Ⅱ)以C为坐标原点建立如图所示空间直角坐标系,由二面角A-PB-C的两个面的法向量所成角的余弦值求得二面角A-PB-C的平面角的余弦值.
解答:
(Ⅰ)证明:如图,
∵点P在平面ABC上的射影是AC的中点,
∴PD⊥平面ABC,又BC?平面ABC,
∴PD⊥BC,
∵BC=2AC=8,AB=4
,
∴AB2=AC2+BC2,
故AC⊥BC.
又AC∩PD=D,
BC⊥平面PAC,BC?平面PBC,
∴平面PBC⊥平面PAC;
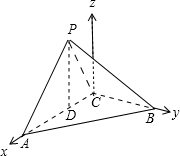
(Ⅱ)如图建立空间直角坐标系,则C(0,0,0),A(4,0,0),B(0,8,0),P(2,0,2
),
=(2,-8,2
),
=(-4,8,0),
=(2,0,2
),
=(0,8,0).
设平面PAB的法向量为
=(x1,y1,z1),
由
,得
,
取y1=1,则z1=2,x1=
,
∴
=(2,1,
).
设平面PBC的一个法向量为
=(x2,y2,z2),
由
,得
,
取y2=0,得z2=1,x2=-
,
∴
=(-
,0,1).
∴cos<
,
>=|
|=
.
∴二面角A-PB-C的平面角的余弦值为
.

∵点P在平面ABC上的射影是AC的中点,
∴PD⊥平面ABC,又BC?平面ABC,
∴PD⊥BC,
∵BC=2AC=8,AB=4
| 5 |
∴AB2=AC2+BC2,
故AC⊥BC.
又AC∩PD=D,
BC⊥平面PAC,BC?平面PBC,
∴平面PBC⊥平面PAC;
(Ⅱ)如图建立空间直角坐标系,则C(0,0,0),A(4,0,0),B(0,8,0),P(2,0,2
| 2 |
| BP |
| 3 |
| AB |
| CP |
| 3 |
| CB |
设平面PAB的法向量为
| n |
由
|
|
取y1=1,则z1=2,x1=
2
| ||
| 3 |
∴
| n |
2
| ||
| 3 |
设平面PBC的一个法向量为
| m |
由
|
|
取y2=0,得z2=1,x2=-
| 3 |
∴
| m |
| 3 |
∴cos<
| m |
| n |
| ||||
|
|
2
| ||
| 19 |
∴二面角A-PB-C的平面角的余弦值为
2
| ||
| 19 |
点评:本题考查面面垂直的判断,考查学生的空间想象能力和思维能力,训练了利用空间向量求二面角的方法,是中档题.

练习册系列答案
相关题目
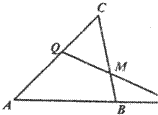 如图,在△ABC中,
如图,在△ABC中,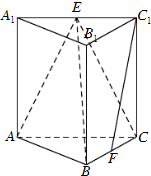 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.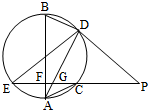 如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.