题目内容
已知抛物线y2=2px(p>0)的焦点为F,点P是抛物线上的一点,且其纵坐标为4,|PF|=4.
(1)求抛物线的方程;
(2)设点A(x1,y1),B(x2,y2)是抛物线上异于点P的两点,∠APB的角平分线与x轴垂直,且线段AB的中垂线与x轴交于点M,求
的最小值.
(1)求抛物线的方程;
(2)设点A(x1,y1),B(x2,y2)是抛物线上异于点P的两点,∠APB的角平分线与x轴垂直,且线段AB的中垂线与x轴交于点M,求
| |MF| |
| |AB| |
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)设出P点坐标(x0,4),由抛物线的定义及点在抛物线上列式求得x0和p的值,则抛物线方程可求;
(2)由(1)求得P点坐标,再由∠APB的角平分线与x轴垂直,可知PA,PB的斜率互为相反数,设出两直线方程,分别和抛物线方程联立后得到A,B的纵坐标,代入A,B的斜率公式求得A,B的斜率,然后写出AB所在直线方程,和抛物线方程联立后由弦长公式求得|AB|,借助于AB的中垂线方程求得|MF|,代入
后整理,然后利用基本不等式求最值.
(2)由(1)求得P点坐标,再由∠APB的角平分线与x轴垂直,可知PA,PB的斜率互为相反数,设出两直线方程,分别和抛物线方程联立后得到A,B的纵坐标,代入A,B的斜率公式求得A,B的斜率,然后写出AB所在直线方程,和抛物线方程联立后由弦长公式求得|AB|,借助于AB的中垂线方程求得|MF|,代入
| |MF| |
| |AB| |
解答:
解:(1)设P(x0,4),
∵|PF|=4,由抛物线定义得:x0+
=4 ①
又42=2px0,
∴x0=
.代入①得,
+
=4,解得:p=4.
∴抛物线方程为y2=8x;
(2)由(1)知,P(2,4),
∵∠APB的角平分线与x轴垂直,
∴PA,PB的倾斜角互补,即PA,PB的斜率互为相反数,
设PA:y-4=k(x-2),k≠0,
联立
,得y2-
y-16+
=0,
则y1+4=
,即y1=
-4.
PB:y-4=-k(x-2),
联立
,得y2+
-16-
=0,
则y2+4=-
,即y2=-
-4.
∴kAB=
=
=
=-1.
设AB:y=-x+b,代入y2=8x,得y2+8y-8b=0.
由△=64+32b>0,得b>-2.
又y1+y2=-8,y1y2=-8b,
∴|AB|=
|y1-y2|=
=8
.
又AB的中垂线方程为y=x-b-8,
则点M的坐标为(b+8,0),
∴|MF|=6+b.
则
=
=
=
≥
.
当且仅当b=2时取等号.
∴
的最小值为
.
∵|PF|=4,由抛物线定义得:x0+
| p |
| 2 |
又42=2px0,
∴x0=
| 8 |
| p |
| 8 |
| p |
| p |
| 2 |
∴抛物线方程为y2=8x;
(2)由(1)知,P(2,4),
∵∠APB的角平分线与x轴垂直,
∴PA,PB的倾斜角互补,即PA,PB的斜率互为相反数,
设PA:y-4=k(x-2),k≠0,
联立
|
| 8 |
| k |
| 32 |
| k |
则y1+4=
| 8 |
| k |
| 8 |
| k |
PB:y-4=-k(x-2),
联立
|
| 8 |
| k |
| 32 |
| k |
则y2+4=-
| 8 |
| k |
| 8 |
| k |
∴kAB=
| y2-y1 |
| x2-x1 |
| y2-y1 | ||||
|
| 8 |
| y2+y1 |
设AB:y=-x+b,代入y2=8x,得y2+8y-8b=0.
由△=64+32b>0,得b>-2.
又y1+y2=-8,y1y2=-8b,
∴|AB|=
| 2 |
| 2 |
| (-8)2+4×8b |
| b+2 |
又AB的中垂线方程为y=x-b-8,
则点M的坐标为(b+8,0),
∴|MF|=6+b.
则
| |MF| |
| |AB| |
| |6+b| | ||
8
|
| 1 |
| 8 |
|
| 1 |
| 8 |
(b+2)+
|
| 1 |
| 2 |
当且仅当b=2时取等号.
∴
| |MF| |
| |AB| |
| 1 |
| 2 |
点评:本题考查了抛物线的方程,考查了直线与圆锥曲线的关系,考查了弦长公式的应用,训练了利用基本不等式求最值,考查了学生的计算能力,是压轴题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在等差数列{an}中,首项a1=0,公差d≠0,若ap=S9,则p的值为( )
| A、37 | B、20 | C、36 | D、9 |
已知Sn是等差数列{an}(n∈N*)的前n项和,且S8>S9>S7,有下列四个命题,期中是假命题的是( )
| A、公差d<0 |
| B、在所有Sn<0中,S17最大 |
| C、a8>a9 |
| D、满足Sn>0的n的个数有15个 |
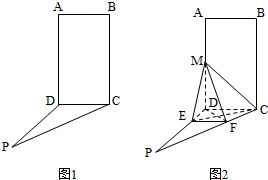 如图1,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2作如图2折叠;折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.
如图1,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2作如图2折叠;折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.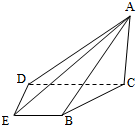 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=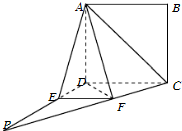 如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.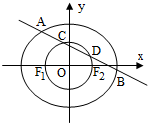 已知椭圆
已知椭圆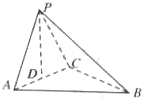 如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4
如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4