题目内容
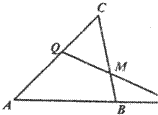 如图,在△ABC中,
如图,在△ABC中,| CM |
. |
| BM |
. |
| AP |
. |
| AB |
. |
| AQ |
. |
| AC |
A、1+
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:首先根据的向量的几何意义,利用P,M,Q三点共线,得出m,n的关系,分别令
=y,
=x,f(x)=m+n,得到关于x的函数关系式,在求导,根据导数求最小值.
| 1 |
| n |
| 1 |
| m |
解答:
解:如图:

∵
=
-
,
=2
,
∴
=
=
(
-
)
∴
=
+
=
+
∵
=m
,
=n
,
∴
=
+
∵P,M,Q三点共线,
∴
+
=1,
令
=y,
=x,
∴
+
=1
∴y=3-2x,
∵x>0,y>0
∴0<x<
,
令f(x)=m+n=
+
=
+
,
∴f′(x)=
-
令f′(x)=0,
∴
=
解得,x=
,或x=
>
(舍去)
当x=
时,f(x)有最小值,
∴f(x)min=1+
,
故选:A.

∵
| BC |
| AC |
| AB |
| CM |
. |
| BM |
∴
| BM |
| 1 |
| 3 |
| BC |
| 1 |
| 3 |
| AC |
| AB |
∴
| AM |
| AB |
| BM |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AB |
∵
. |
| AP |
. |
| AB |
. |
| AQ |
. |
| AC |
∴
| AM |
| 1 |
| 3n |
| AQ |
| 2 |
| 3m |
| AP |
∵P,M,Q三点共线,
∴
| 1 |
| 3n |
| 2 |
| 3m |
令
| 1 |
| n |
| 1 |
| m |
∴
| y |
| 3 |
| 2x |
| 3 |
∴y=3-2x,
∵x>0,y>0
∴0<x<
| 3 |
| 2 |
令f(x)=m+n=
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| 3-2x |
∴f′(x)=
| 2 |
| (3-2x)2 |
| 1 |
| x2 |
令f′(x)=0,
∴
| 2 |
| (3-2x)2 |
| 1 |
| x2 |
解得,x=
6-3
| ||
| 2 |
6+3
| ||
| 2 |
| 3 |
| 2 |
当x=
6-3
| ||
| 2 |
∴f(x)min=1+
2
| ||
| 3 |
故选:A.
点评:本题考查了向量的几何意义以及三点共线定理以及利用到导数来求函数的最小值问题,是一道综合题目,涉及知识点比较多,考查了化归思想,方程的思想.属于难题.

练习册系列答案
相关题目
抛物线y2=2px(p>0)的焦点为F,已知A,B为抛物线上的两个动点,且满足∠AFB=120°,过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则
的最大值为( )
| |MN| |
| |AB| |
| A、2 | ||||
B、
| ||||
| C、1 | ||||
D、
|
在等差数列{an}中,首项a1=0,公差d≠0,若ap=S9,则p的值为( )
| A、37 | B、20 | C、36 | D、9 |
设a>0,在二项式(a-
)10的展开式中,含x的项的系数与含x4的项的系数相等,则a的值为( )
| x |
| A、1 | B、2 | C、4 | D、8 |
复数
的共轭复数是( )
| 5 |
| 3-4i |
A、
| ||||
B、
| ||||
| C、3+4i | ||||
| D、3-4i |
已知Sn是等差数列{an}(n∈N*)的前n项和,且S8>S9>S7,有下列四个命题,期中是假命题的是( )
| A、公差d<0 |
| B、在所有Sn<0中,S17最大 |
| C、a8>a9 |
| D、满足Sn>0的n的个数有15个 |
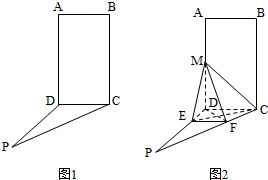 如图1,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2作如图2折叠;折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.
如图1,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2作如图2折叠;折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.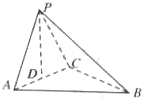 如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4
如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4