题目内容
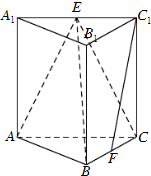 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.(Ⅰ)求证:平面ABE⊥B1BCC1;
(Ⅱ)求证:C1F∥平面ABE;
(Ⅲ)求三棱锥E-ABC的体积.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离,空间角,立体几何
分析:(Ⅰ)证明AB⊥B1BCC1,可得平面ABE⊥B1BCC1;
(Ⅱ)证明C1F∥平面ABE,只需证明四边形FGEC1为平行四边形,可得C1F∥EG;
(Ⅲ)利用VE-ABC=
S△ABC•AA1,可求三棱锥E-ABC的体积.
(Ⅱ)证明C1F∥平面ABE,只需证明四边形FGEC1为平行四边形,可得C1F∥EG;
(Ⅲ)利用VE-ABC=
| 1 |
| 3 |
解答:
 (Ⅰ)证明:∵三棱柱ABC-A1B1C1中,侧棱垂直于底面,
(Ⅰ)证明:∵三棱柱ABC-A1B1C1中,侧棱垂直于底面,
∴BB1⊥AB,
∵AB⊥BC,BB1∩BC=B,
∴AB⊥平面B1BCC1,
∵AB?平面ABE,
∴平面ABE⊥B1BCC1;
(Ⅱ)证明:取AB中点G,连接EG,FG,则,
∵F是BC的中点,
∴FG∥AC,FG=
AC,
∵E是A1C1的中点,
∴FG∥EC1,FG=EC1,
∴四边形FGEC1为平行四边形,
∴C1F∥EG,
∵C1F?平面ABE,EG?平面ABE,
∴C1F∥平面ABE;
(Ⅲ)解:∵AA1=AC=2,BC=1,AB⊥BC,
∴AB=
,
∴VE-ABC=
S△ABC•AA1=
×
×
×1×2=
.
 (Ⅰ)证明:∵三棱柱ABC-A1B1C1中,侧棱垂直于底面,
(Ⅰ)证明:∵三棱柱ABC-A1B1C1中,侧棱垂直于底面,∴BB1⊥AB,
∵AB⊥BC,BB1∩BC=B,
∴AB⊥平面B1BCC1,
∵AB?平面ABE,
∴平面ABE⊥B1BCC1;
(Ⅱ)证明:取AB中点G,连接EG,FG,则,
∵F是BC的中点,
∴FG∥AC,FG=
| 1 |
| 2 |
∵E是A1C1的中点,
∴FG∥EC1,FG=EC1,
∴四边形FGEC1为平行四边形,
∴C1F∥EG,
∵C1F?平面ABE,EG?平面ABE,
∴C1F∥平面ABE;
(Ⅲ)解:∵AA1=AC=2,BC=1,AB⊥BC,
∴AB=
| 3 |
∴VE-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
点评:本题考查线面平行、垂直的证明,考查三棱锥E-ABC的体积的计算,正确运用线面平行、垂直的判定定理是关键.

练习册系列答案
相关题目
复数
的共轭复数是( )
| 5 |
| 3-4i |
A、
| ||||
B、
| ||||
| C、3+4i | ||||
| D、3-4i |
以边长为1的正方形的一边所在所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于( )
| A、2π | B、π | C、2 | D、1 |
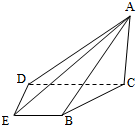 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=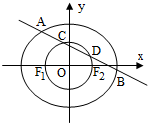 已知椭圆
已知椭圆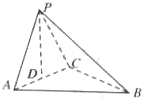 如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4
如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4