题目内容
设函数f(x)=|x+
|+|x-a|(a>0).
(Ⅰ)证明:f(x)≥2;
(Ⅱ)若f(3)<5,求a的取值范围.
| 1 |
| a |
(Ⅰ)证明:f(x)≥2;
(Ⅱ)若f(3)<5,求a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)由a>0,f(x)=|x+
|+|x-a|,利用绝对值三角不等式、基本不等式证得f(x)≥2成立.
(Ⅱ)由f(3)=|3+
|+|3-a|<5,分当a>3时和当0<a≤3时两种情况,分别去掉绝对值,求得不等式的解集,再取并集,即得所求.
| 1 |
| a |
(Ⅱ)由f(3)=|3+
| 1 |
| a |
解答:
解:(Ⅰ)证明:∵a>0,f(x)=|x+
|+|x-a|≥|(x+
)-(x-a)|=|a+
|=a+
≥2
=2,
故不等式f(x)≥2成立.
(Ⅱ)∵f(3)=|3+
|+|3-a|<5,
∴当a>3时,不等式即a+
<5,即a2-5a+1<0,解得3<a<
.
当0<a≤3时,不等式即 6-a+
<5,即 a2-a-1>0,求得
<a≤3.
综上可得,a的取值范围(
,
).
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
a•
|
故不等式f(x)≥2成立.
(Ⅱ)∵f(3)=|3+
| 1 |
| a |
∴当a>3时,不等式即a+
| 1 |
| a |
5+
| ||
| 2 |
当0<a≤3时,不等式即 6-a+
| 1 |
| a |
1+
| ||
| 2 |
综上可得,a的取值范围(
1+
| ||
| 2 |
5+
| ||
| 2 |
点评:本题主要考查绝对值三角不等式,绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知Sn是等差数列{an}(n∈N*)的前n项和,且S8>S9>S7,有下列四个命题,期中是假命题的是( )
| A、公差d<0 |
| B、在所有Sn<0中,S17最大 |
| C、a8>a9 |
| D、满足Sn>0的n的个数有15个 |
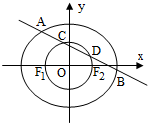 已知椭圆
已知椭圆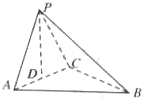 如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4
如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4