题目内容
在以O为极点的极坐标系中，圆ρ=4sinθ和直线ρsinθ=a相交于A、B两点，若△AOB是等边三角形，则a的值为 ．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把极坐标方程化为直角坐标方程，求出B的坐标的值，代入x2+（y-2）2=4，可得a的值．
解答：
解：直线ρsinθ=a即y=a，（a＞0），曲线ρ=4sinθ，
即ρ2=4ρsinθ，即x2+（y-2）2=4，表示以C（0，2）为圆心，以2为半径的圆，
∵△AOB是等边三角形，∴B（
a，a），
代入x2+（y-2）2=4，可得（
a）2+（a-2）2=4，
∵a＞0，∴a=3．
故答案为：3．
即ρ2=4ρsinθ，即x2+（y-2）2=4，表示以C（0，2）为圆心，以2为半径的圆，
∵△AOB是等边三角形，∴B（
| ||
| 3 |
代入x2+（y-2）2=4，可得（
| ||
| 3 |
∵a＞0，∴a=3．
故答案为：3．
点评：本题考查把极坐标方程化为直角坐标方程的方法，直线和圆的位置关系，求出B的坐标是解题的关键，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
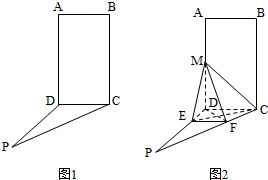如图1，四边形ABCD为矩形，PD⊥平面ABCD，AB=1，BC=PC=2作如图2折叠；折痕EF∥DC，其中点E，F分别在线段PD，PC上，沿EF折叠后点P叠在线段AD上的点记为M，并且MF⊥CF．
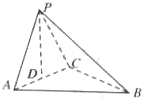如图，在三棱锥P-ABC中，点P在平面ABC上的射影D是AC的中点，BC=2AC=8，AB=4已知底面边长为1，侧棱长为
的正四棱柱的各顶点均在同一球面上，则该球的体积为（ ）
| 2 |
A、
| ||
| B、4π | ||
| C、2π | ||
D、
|