题目内容
已知函数f(x)=2x3-3x.
(Ⅰ)求f(x)在区间[-2,1]上的最大值;
(Ⅱ)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围;
(Ⅲ)问过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)
(Ⅰ)求f(x)在区间[-2,1]上的最大值;
(Ⅱ)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围;
(Ⅲ)问过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)
考点:导数在最大值、最小值问题中的应用,函数的零点,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)利用导数求得极值点比较f(-2),f(-
),f(
),f(1)的大小即得结论;
(Ⅱ)利用导数的几何意义得出切线方程4
-6
+t+3=0,设g(x)=4x3-6x2+t+3,则“过点P(1,t)存在3条直线与曲线y=f(x)相切”,
等价于“g(x)有3个不同的零点”.利用导数判断函数的单调性进而得出函数的零点情况,得出结论;
(Ⅲ)利用(Ⅱ)的结论写出即可.
| ||
| 2 |
| ||
| 2 |
(Ⅱ)利用导数的几何意义得出切线方程4
| x | 3 0 |
| x | 2 0 |
等价于“g(x)有3个不同的零点”.利用导数判断函数的单调性进而得出函数的零点情况,得出结论;
(Ⅲ)利用(Ⅱ)的结论写出即可.
解答:
解:(Ⅰ)由f(x)=2x3-3x得f′(x)=6x2-3,
令f′(x)=0得,x=-
或x=
,
∵f(-2)=-10,f(-
)=
,f(
)=-
,f(1)=-1,
∴f(x)在区间[-2,1]上的最大值为
.
(Ⅱ)设过点P(1,t)的直线与曲线y=f(x)相切于点(x0,y0),
则y0=2
-3x0,且切线斜率为k=6
-3,
∴切线方程为y-y0=(6
-3)(x-x0),
∴t-y0=(6
-3)(1-x0),
即4
-6
+t+3=0,
设g(x)=4x3-6x2+t+3,
则“过点P(1,t)存在3条直线与曲线y=f(x)相切”,等价于“g(x)有3个不同的零点”.
∵g′(x)=12x2-12x=12x(x-1),
∴g(x)与g′(x)变化情况如下:
∴g(0)=t+3是g(x)的极大值,g(1)=t+1是g(x)的极小值.
当g(0)=t+3≤0,即t≤-3时,g(x)在区间(-∞,1]和(1,+∞)上分别至多有一个零点,故g(x)至多有2个零点.
当g(1)=t+1≥0,即t≥-1时,g(x)在区间(-∞,0]和(0,+∞)上分别至多有一个零点,故g(x)至多有2个零点.
当g(0)>0且g(1)<0,即-3<t<-1时,∵g(-1)=t-7<0,g(2)=t+11>0,
∴g(x)分别在区间[-1,0),[0,1)和[1,2)上恰有1个零点,由于g(x)在区间(-∞,0)和[1,+∞)上单调,
故g(x)分别在区间(-∞,0)和[1,+∞)上恰有1个零点.
综上所述,当过点过点P(1,t)存在3条直线与曲线y=f(x)相切时,t的取值范围是(-3,-1).
(Ⅲ)过点A(-1,2)存在3条直线与曲线y=f(x)相切;
过点B(2,10)存在2条直线与曲线y=f(x)相切;
过点C(0,2)存在1条直线与曲线y=f(x)相切.
令f′(x)=0得,x=-
| ||
| 2 |
| ||
| 2 |
∵f(-2)=-10,f(-
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
∴f(x)在区间[-2,1]上的最大值为
| 2 |
(Ⅱ)设过点P(1,t)的直线与曲线y=f(x)相切于点(x0,y0),
则y0=2
| x | 3 0 |
| x | 2 0 |
∴切线方程为y-y0=(6
| x | 2 0 |
∴t-y0=(6
| x | 2 0 |
即4
| x | 3 0 |
| x | 2 0 |
设g(x)=4x3-6x2+t+3,
则“过点P(1,t)存在3条直线与曲线y=f(x)相切”,等价于“g(x)有3个不同的零点”.
∵g′(x)=12x2-12x=12x(x-1),
∴g(x)与g′(x)变化情况如下:
| x | (-∞,0) | 0 | (0,1) | 1 | (1,+∞) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | t+3 | ↘ | t+1 | ↗ |
当g(0)=t+3≤0,即t≤-3时,g(x)在区间(-∞,1]和(1,+∞)上分别至多有一个零点,故g(x)至多有2个零点.
当g(1)=t+1≥0,即t≥-1时,g(x)在区间(-∞,0]和(0,+∞)上分别至多有一个零点,故g(x)至多有2个零点.
当g(0)>0且g(1)<0,即-3<t<-1时,∵g(-1)=t-7<0,g(2)=t+11>0,
∴g(x)分别在区间[-1,0),[0,1)和[1,2)上恰有1个零点,由于g(x)在区间(-∞,0)和[1,+∞)上单调,
故g(x)分别在区间(-∞,0)和[1,+∞)上恰有1个零点.
综上所述,当过点过点P(1,t)存在3条直线与曲线y=f(x)相切时,t的取值范围是(-3,-1).
(Ⅲ)过点A(-1,2)存在3条直线与曲线y=f(x)相切;
过点B(2,10)存在2条直线与曲线y=f(x)相切;
过点C(0,2)存在1条直线与曲线y=f(x)相切.
点评:本题主要考查利用导数求切线方程及判断函数的单调性求最值等知识,考查转化划归思想及分类讨论思想的运用能力和运算能力,属难题.

练习册系列答案
相关题目
设a>0,在二项式(a-
)10的展开式中,含x的项的系数与含x4的项的系数相等,则a的值为( )
| x |
| A、1 | B、2 | C、4 | D、8 |
已知底面边长为1,侧棱长为
的正四棱柱的各顶点均在同一球面上,则该球的体积为( )
| 2 |
A、
| ||
| B、4π | ||
| C、2π | ||
D、
|
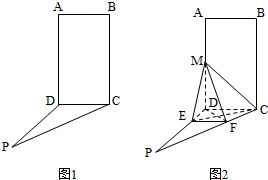 如图1,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2作如图2折叠;折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.
如图1,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2作如图2折叠;折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.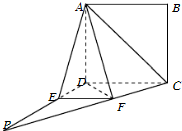 如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.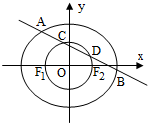 已知椭圆
已知椭圆 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.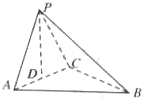 如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4
如图,在三棱锥P-ABC中,点P在平面ABC上的射影D是AC的中点,BC=2AC=8,AB=4