题目内容
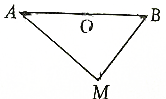 如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明
如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明| MA |
| MB |
| MO |
| MO |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:根据向量加法的三角形法则,以及相反向量的概念即可完成证明.
解答:
证明:如图连接MO,

=
+
,
=
+
;
∵O是AB的中点;
∴
+
=
;
∴
+
=
+
.

| MA |
| MO |
| OA |
| MB |
| MO |
| OB |
∵O是AB的中点;
∴
| OA |
| OB |
| 0 |
∴
| MA |
| MB |
| MO |
| MO |
点评:考查向量加法的三角形法则,以及相反向量的概念,也可用向量加法的平行四边形法则证明.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
存在下列三个命题:
①“等边三角形的三个内角都是60°”的逆命题;
②“若k>0,则一元二次方程x2+2x-k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题.
其中真命题的个数是( )
①“等边三角形的三个内角都是60°”的逆命题;
②“若k>0,则一元二次方程x2+2x-k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题.
其中真命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
在△ABC中,若cosC=2sinAsinB-1,sin2A+sin2B=1,则此三角形为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
已知向量
=(-1,2,4),
=(x,-1,-2),并且
⊥
,则实数x的值为( )
| a |
| b |
| a |
| b |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
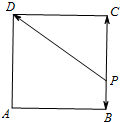 如图,正方形ABCD的边长为2,点P是线段BC上的动点,则(
如图,正方形ABCD的边长为2,点P是线段BC上的动点,则(