题目内容
已知在△ABC中,a,b,c分别是角A,B,C的对边,且满足4cosC+cos2C=4cosCcos2
.
(Ⅰ)求∠C的大小;
(Ⅱ)若|
-
|=2,求△ABC面积的最大值.
| C |
| 2 |
(Ⅰ)求∠C的大小;
(Ⅱ)若|
| CA |
| 1 |
| 2 |
| CB |
考点:平面向量数量积的运算,正弦定理
专题:计算题,三角函数的求值,解三角形,不等式的解法及应用
分析:(Ⅰ)运用二倍角公式化简,结合特殊角的三角函数值,即可得到C;
(Ⅱ)运用向量的平方即为模的平方,和向量的数量积的定义,结合重要不等式,求得ab的最大值为8,再由三角形的面积公式计算即可得到所求值.
(Ⅱ)运用向量的平方即为模的平方,和向量的数量积的定义,结合重要不等式,求得ab的最大值为8,再由三角形的面积公式计算即可得到所求值.
解答:
解:(Ⅰ)4cosC+cos2C=4cosCcos2
,
即有4cosC+2cos2C-1=2cosC(1+cosC),
则有cosC=
,
由C为三角形的内角,则C=
;
(Ⅱ)|
-
|=2,即有(
-
)2=4,
即
2-
•
+
2=4,
即有b2+
a2-
ba=4,
由于b2+
a2≥2b•
a=ab,
则有4+
ab≥ab,即ab≤8.
当且仅当b=
a时,取得等号.
则△ABC的面积S=
absinC≤
×8×
=2
.
则三角形ABC的面积的最大值为2
.
| C |
| 2 |
即有4cosC+2cos2C-1=2cosC(1+cosC),
则有cosC=
| 1 |
| 2 |
由C为三角形的内角,则C=
| π |
| 3 |
(Ⅱ)|
| CA |
| 1 |
| 2 |
| CB |
| CA |
| 1 |
| 2 |
| CB |
即
| CA |
| CA |
| CB |
| 1 |
| 4 |
| CB |
即有b2+
| 1 |
| 4 |
| 1 |
| 2 |
由于b2+
| 1 |
| 4 |
| 1 |
| 2 |
则有4+
| 1 |
| 2 |
当且仅当b=
| 1 |
| 2 |
则△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
则三角形ABC的面积的最大值为2
| 3 |
点评:本题考查平面向量的数量积的定义和性质,考查三角形的面积公式,以及三角函数的化简和求值,考查运算能力,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
在区间[3,5]上任取一个数m,则“函数f(x)=x2-4x-m+4(-1≤x<4)有两个零点”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题正确的是( )
| A、经过三点确定一个平面 |
| B、经过一条直线和一个点确定一个平面 |
| C、两两相交且不共点的三条直线确定一个平面 |
| D、四边形确定一个平面 |
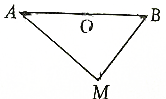 如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明
如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明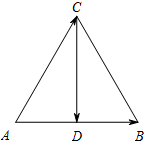 如图,已知正三角形ABC的边长为1,设
如图,已知正三角形ABC的边长为1,设