题目内容
已知圆O以原点为圆心,且与直线5x-12y+26=0相切.
(1)求圆O的方程;
(2)若直线l过点(1,2),且被圆O截得的弦长为2
,求直线l的方程;
(3)由圆O上任意一点M向x轴作垂线,垂足为N,P是直线MN上一点且满足|NP|=2|PM|,求点P的轨迹方程.
(1)求圆O的方程;
(2)若直线l过点(1,2),且被圆O截得的弦长为2
| 3 |
(3)由圆O上任意一点M向x轴作垂线,垂足为N,P是直线MN上一点且满足|NP|=2|PM|,求点P的轨迹方程.
考点:直线和圆的方程的应用,轨迹方程
专题:综合题,直线与圆
分析:(1)求出圆心到直线5x-12y+26=0的距离,得到半径,即可求圆O的方程;
(2)求出圆心到直线l的距离为
=1,利用直线l过点(1,2),分类讨论,即可求直线l的方程;
(3)设P(x,y),M(x,y′),N(x,0),利用|NP|=2|PM|,确定M,P坐标之间的关系,即可求点P的轨迹方程.
(2)求出圆心到直线l的距离为
| 4-3 |
(3)设P(x,y),M(x,y′),N(x,0),利用|NP|=2|PM|,确定M,P坐标之间的关系,即可求点P的轨迹方程.
解答:
解:(1)圆心到直线5x-12y+26=0的距离d=
=2,
∴圆O的方程为x2+y2=4;
(2)∵直线l被圆O截得的弦长为2
,
∴圆心到直线l的距离为
=1,
∵直线l过点(1,2),
∴斜率不存在时,直线l的方程x=1满足;
斜率存在时,设直线的方程为y-2=k(x-1),即kx-y-k+2=0,
∴圆心到直线l的距离
=1,
∴k=
,
∴直线l的方程为3x-4y-5=0,
综上所述,直线l的方程为x=1或3x-4y-5=0;
(3)设P(x,y),M(x,y′),N(x,0),则
①
=2
,可得(0,y)=2(x,y′-y),∴y′=
y,
∵M在圆上,
∴x2+
y2=4;
②
=-2
,可得(0,y)=-2(x,y′-y),∴y′=
y,
∵M在圆上,
∴x2+
y2=4.
| 26 |
| 13 |
∴圆O的方程为x2+y2=4;
(2)∵直线l被圆O截得的弦长为2
| 3 |
∴圆心到直线l的距离为
| 4-3 |
∵直线l过点(1,2),
∴斜率不存在时,直线l的方程x=1满足;
斜率存在时,设直线的方程为y-2=k(x-1),即kx-y-k+2=0,
∴圆心到直线l的距离
| |-k+2| | ||
|
∴k=
| 3 |
| 4 |
∴直线l的方程为3x-4y-5=0,
综上所述,直线l的方程为x=1或3x-4y-5=0;
(3)设P(x,y),M(x,y′),N(x,0),则
①
| NP |
| PM |
| 3 |
| 2 |
∵M在圆上,
∴x2+
| 9 |
| 4 |
②
| NP |
| PM |
| 1 |
| 2 |
∵M在圆上,
∴x2+
| 1 |
| 4 |
点评:本题考查轨迹方程,考查直线与圆的位置关系,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列命题正确的是( )
| A、经过三点确定一个平面 |
| B、经过一条直线和一个点确定一个平面 |
| C、两两相交且不共点的三条直线确定一个平面 |
| D、四边形确定一个平面 |
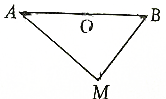 如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明
如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明