题目内容
存在下列三个命题:
①“等边三角形的三个内角都是60°”的逆命题;
②“若k>0,则一元二次方程x2+2x-k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题.
其中真命题的个数是( )
①“等边三角形的三个内角都是60°”的逆命题;
②“若k>0,则一元二次方程x2+2x-k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题.
其中真命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:①利用逆命题的意义即可得出,再利用等边三角形的定义即可得出;
②利用逆否命题的定义即可得出,再利用一元二次方程的是否有实数根与判别式的关系即可得出;
③利用否命题的意义即可得出,进而判断出真假.
②利用逆否命题的定义即可得出,再利用一元二次方程的是否有实数根与判别式的关系即可得出;
③利用否命题的意义即可得出,进而判断出真假.
解答:
解:①“等边三角形的三个内角均为60°”的逆命题为“三个内角均为60°的三角形是等边三角形”,正确;
②若k>0,则方程x2+2x-k=0有实根”的逆否命题是“方程x2+2x-k=0没有实根,则k≤0”,
对于逆否命题:方程x2+2x-k=0没有实根,则△=4+4k<0,解得k<-1,∴k≤0,因此正确;
③“全等三角形的面积相等”的否命题是“不全等的三角形的面积不相等”,不正确.
综上可知:只有①②正确.
故选:C.
②若k>0,则方程x2+2x-k=0有实根”的逆否命题是“方程x2+2x-k=0没有实根,则k≤0”,
对于逆否命题:方程x2+2x-k=0没有实根,则△=4+4k<0,解得k<-1,∴k≤0,因此正确;
③“全等三角形的面积相等”的否命题是“不全等的三角形的面积不相等”,不正确.
综上可知:只有①②正确.
故选:C.
点评:本题考查命题的真假判断与应用,考查了四种命题的定义及其之间的关系,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知全集U=R,集合A={x|1≤x≤3},B={x|x>2},则A∩∁UB等于( )
| A、{x|1<x≤2} |
| B、{x|1≤x<2} |
| C、{x|1≤x≤2} |
| D、{x|1≤x≤3} |
函数f(x)=
的单调递增区间为( )
| lnx |
| x |
| A、(-∞,0)和(0,e) |
| B、(-∞,0)和(e,+∞) |
| C、(0,e) |
| D、(e,+∞) |
已知函数f(x)是奇函数,且f(x)=
,当2≤x<3时,f(x)=(
)x,则f(2014)=( )
| 1 |
| f(x+3) |
| 1 |
| 2 |
| A、2 | ||
| B、4 | ||
| C、-4 | ||
D、-
|
在区间[3,5]上任取一个数m,则“函数f(x)=x2-4x-m+4(-1≤x<4)有两个零点”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
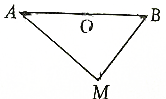 如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明
如图所示,已知O是线段AB的中点,M是平面上任意一点,试证明