题目内容
4.下列四个命题申是真命题的是①③④(填所有真命题的序号)①“p∧q为真”是“p∨q为真”的充分不必要条件;
②空间中一个角的两边和另一个角的两边分别平行,则这两个角相等;
③在侧棱长为2,底面边长为3的正三棱锥中,侧棱与底面成30°的角;
④动圆P过定点A(-2,0),且在定圆B:(x-2)2+y2=36的内部与其相内切,则动圆圆心P的轨迹为一个椭圆.
分析 ①根据充分条件和必要条件的定义结合复合命题的真假关系进行判断.
②根据空间角的平行定理进行判断.
③根据线面所成角的定义进行求解判断.
④根据圆与的内切关系以及椭圆的定义进行判断.
解答 解:①“p∧q为真”,则p,q同时为真命题,则“p∨q为真”,
当p真q假时,满足p∨q为真,但p∧q为假,则“p∧q为真”是“p∨q为真”的充分不必要条件正确,故①正确;
②空间中一个角的两边和另一个角的两边分别平行,则这两个角相等或互补;故②错误,
③设正三棱锥为P-ABC,顶点P在底面的射影为O,则O为△ABC的中心,∠PCO为侧棱与底面所成角
∵正三棱锥的底面边长为3,∴CO=$\frac{\sqrt{3}}{3}×3=\sqrt{3}$
∵侧棱长为2,∴$PO=\sqrt{4-3}=1$
在直角△POC中,tan∠PCO=$\frac{PO}{CO}=\frac{\sqrt{3}}{3}$
∴侧棱与底面所成角的正切值为$\frac{\sqrt{3}}{3}$,即侧棱与底面所成角为30°,故③正确,
④如图,设动圆P和定圆B内切于M,则动圆的圆心P到两点,即定点A(-2,0)和定圆的圆心B(2,0)的距离之和恰好等于定圆半径,
即|PA|+|PB|=|PM|+|PB|=|BM|=6>4=|AB|.
∴点P的轨迹是以A、B为焦点的椭圆,
故动圆圆心P的轨迹为一个椭圆,故④正确,
故答案为:①③④
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.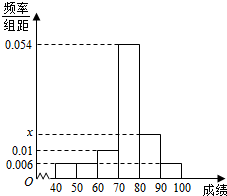 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )
 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )| A. | 75.5 | B. | 75.2 | C. | 75.1 | D. | 75.3 |
19.O为坐标原点,F为抛物线$C:y=\frac{1}{4}{x^2}$的焦点,P是抛物线C上一点,若|PF|=4,则△POF的面积为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
9.函数f(x)=3sin(2x-$\frac{π}{3}$)的图象的一条对称轴是( )
| A. | $x=\frac{π}{3}$ | B. | $x=\frac{5π}{12}$ | C. | $x=\frac{π}{2}$ | D. | $x=\frac{5π}{6}$ |
14.已知x∈(0,π),且$cos(x-\frac{π}{4})=\frac{1}{3}$,则tanx=( )
| A. | $-\frac{{9+4\sqrt{2}}}{7}或-\frac{{9-4\sqrt{2}}}{7}$ | B. | $-\frac{{18+8\sqrt{2}}}{7}或-\frac{{18-8\sqrt{2}}}{7}$ | ||
| C. | $-\frac{{9+4\sqrt{2}}}{7}$ | D. | $-\frac{{9-4\sqrt{2}}}{7}$ |
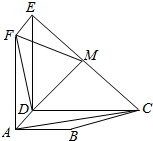 如图,四边形ABCD是梯形,AB∥CD,∠ADC=90°,四边形ADEF是矩形,且平面
如图,四边形ABCD是梯形,AB∥CD,∠ADC=90°,四边形ADEF是矩形,且平面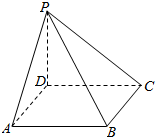 已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.
已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.