题目内容
14. 如图,四边形ABCD是梯形,AB∥CD,∠ADC=90°,四边形ADEF是矩形,且平面
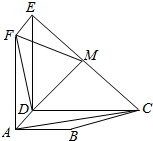
如图,四边形ABCD是梯形,AB∥CD,∠ADC=90°,四边形ADEF是矩形,且平面ABCD丄平面ADEF,AB=AD=1,DE=CD=2,M是线段CE的中点.
(Ⅰ)求证:AC∥平面DMF;
(Ⅱ)求平面DMF与平面ABCD所成角的余弦值.
分析 (Ⅰ)连接AE与DF交于点N.则点N是AE的中点,连结MN,利用三角形中位线定理能够证明AC∥平面DMF.
(Ⅱ)分别以D点为坐标原点建立空间直角坐标系,利用向量法能求出平面MDF与平面ABCD所成锐二面角的余弦值.
解答 (Ⅰ)证明:连接AE与DF交于点N,连结MN,则点N是AE的中点
又M是线段CE的中点
∴MN∥AC----------------------(2分)
又AC?平面DMF,MN?平面DMF,
∴AC∥平面DMF-----------------(4分)
(Ⅱ)解:四边形ADEF是矩形,∴DE⊥AD
又平面ABCD丄平面ADEF,平面ABCD∩平面ADEF=AD
∴DE⊥平面ABCD,
∴DE⊥CD,
∵∠ADC=90°,
∴DE,DC,DA两两垂直
以D点为坐标原点建立空间直角坐标系-----(6分)
则D(0,0,0),F(1,0,2),M(0,1,1)----(7分)
则$\overrightarrow{DF}$=(1,0,2),$\overrightarrow{DM}$=(0,1,1)
设平面DMF的一个法向量为$\overrightarrow{m}$=(x,y,z)
∴$\left\{\begin{array}{l}{x+2z=0}\\{y+z=0}\end{array}\right.$
取$\overrightarrow{m}$=(2,1,-1)---------------(9分)
取平面ABCD的一个法向量为$\overrightarrow{n}$=(0,0,1)---------------(10分)
设平面DNF与平面ABCD所成角为θ
∴cosθ=|$\frac{-1}{\sqrt{4+1+1}}$|=$\frac{\sqrt{6}}{6}$------------(12分)
点评 本题考查直线与平面平行的确定及证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

| A. | 5π | B. | 7π | C. | 9π | D. | 11π |
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4$\sqrt{2}$ |
| A. | 1:1:2 | B. | 1:$\sqrt{2}$:1 | C. | 1:1:1 | D. | 1:1:$\sqrt{2}$ |
| A. | 若m∥α,n∥β,m⊥n,则α⊥β | B. | 若m∥n,n∥α,α∥β,则m∥β | ||
| C. | 若α⊥β,α∩β=n,m⊥n,则m⊥α | D. | 若α∩β=n,m∥α,m∥β,则m∥n |
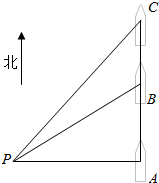 已知在观测点P处测得在正东方向A处一轮船正在沿正北方向匀速航行,经过1小时后在观测点P测得轮船位于北偏东60°方向B处,又经过t小时发现该轮船在北偏东45°方向C处,则t=$\sqrt{3}-1$.
已知在观测点P处测得在正东方向A处一轮船正在沿正北方向匀速航行,经过1小时后在观测点P测得轮船位于北偏东60°方向B处,又经过t小时发现该轮船在北偏东45°方向C处,则t=$\sqrt{3}-1$.