题目内容
9.函数f(x)=3sin(2x-$\frac{π}{3}$)的图象的一条对称轴是( )| A. | $x=\frac{π}{3}$ | B. | $x=\frac{5π}{12}$ | C. | $x=\frac{π}{2}$ | D. | $x=\frac{5π}{6}$ |
分析 由条件利用正弦函数的图象的对称性,得出结论.
解答 解:对于函数$f(x)=3sin(2x-\frac{π}{3})$的图象,令2x-$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,求得x=$\frac{kπ}{2}$+$\frac{5π}{12}$,
故它的图象的一条对称轴是x=$\frac{5π}{12}$,
故选:B.
点评 本题主要考查正弦函数的图象的对称性,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
20.过点(0,2b)的直线l与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的一条斜率为正值的渐近线平行,若双曲线C的右支上的点到直线l的距离恒大于b,则双曲线C的离心率的取值范围是( )
| A. | (1,2] | B. | (2,+∞) | C. | (1,2) | D. | (1,$\sqrt{2}$] |
17.“$\frac{1}{x}$<3”是“x>$\frac{1}{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知实数a>1,命题p:函数$y=lo{g_{\frac{1}{2}}}({x^2}+2x+a)$的定义域为R,命题q:|x|<1是x<a的充分不必要条件,则( )
| A. | p或q为真命题 | B. | p且q为假命题 | C. | ¬p且q为真命题 | D. | ¬p或¬q为真命题 |
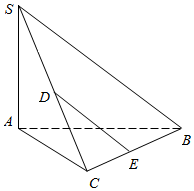 如图,在三棱锥S-ABC中,SA⊥底面ABC,BC⊥AC,D、E分别是SC、BC的中点.
如图,在三棱锥S-ABC中,SA⊥底面ABC,BC⊥AC,D、E分别是SC、BC的中点.