题目内容
19.O为坐标原点,F为抛物线$C:y=\frac{1}{4}{x^2}$的焦点,P是抛物线C上一点,若|PF|=4,则△POF的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据抛物线方程求得抛物线的准线方程与焦点坐标,利用|PF|=4,求得P点的纵坐标,代入抛物线方程求得横坐标,代入三角形面积公式计算即可得到.
解答 解:由抛物线方程得准线方程为:y=-1,焦点F(0,1),
又P为C上一点,|PF|=4,
可得yP=3,
代入抛物线方程得:|xP|=2$\sqrt{3}$,
∴S△POF=$\frac{1}{2}$|0F|•|xP|=$\sqrt{3}$.
故选:C.
点评 本题考查了抛物线的定义及几何性质,熟练掌握抛物线上的点所满足的条件是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.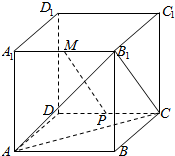 如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )
如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )
 如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )
如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{6}}]$ | B. | $[{\sqrt{6},2\sqrt{2}}]$ | C. | $[{\sqrt{6,}2\sqrt{3}}]$ | D. | $[{\sqrt{6,}3}]$ |
9.在△ABC中,∠C=$\frac{π}{6}$,AC=2$\sqrt{3}$,AB=2,则BC的长是( )
| A. | 2 | B. | 4 | C. | 2或4 | D. | 4或8 |
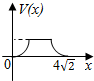
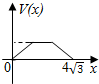
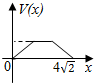
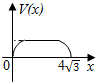
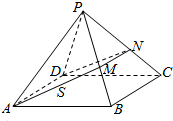 在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )
在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )