题目内容
14.已知x∈(0,π),且$cos(x-\frac{π}{4})=\frac{1}{3}$,则tanx=( )| A. | $-\frac{{9+4\sqrt{2}}}{7}或-\frac{{9-4\sqrt{2}}}{7}$ | B. | $-\frac{{18+8\sqrt{2}}}{7}或-\frac{{18-8\sqrt{2}}}{7}$ | ||
| C. | $-\frac{{9+4\sqrt{2}}}{7}$ | D. | $-\frac{{9-4\sqrt{2}}}{7}$ |
分析 由和差角的公式化简可得cosx+sinx=$\frac{\sqrt{2}}{3}$,结合cos2x+sin2x=1和x的范围可得sinx和cosx的值,可得tanx.
解答 解:∵$cos(x-\frac{π}{4})=\frac{1}{3}$,
∴$\frac{\sqrt{2}}{2}$cosx+$\frac{\sqrt{2}}{2}$sinx=$\frac{1}{3}$,
∴cosx+sinx=$\frac{\sqrt{2}}{3}$,
又cos2x+sin2x=1,x∈(0,π),
∴sinx>0,
联立解得sinx=$\frac{\sqrt{2}+4}{6}$,cosx=$\frac{\sqrt{2}-4}{6}$,
∴tanx=$\frac{sinx}{cosx}$=$-\frac{{9+4\sqrt{2}}}{7}$.
故选:C.
点评 本题考查同角三角函数的基本关系,以及和差角的三角函数公式,属基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
5.已知全集U=R,集合A={x|($\frac{1}{2}$)x≤1,B={x|x2-6x+8≤0},则A∩B为( )
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
9.在△ABC中,∠C=$\frac{π}{6}$,AC=2$\sqrt{3}$,AB=2,则BC的长是( )
| A. | 2 | B. | 4 | C. | 2或4 | D. | 4或8 |
4.与如图所示的图象相符的函数是( )
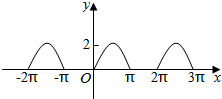

| A. | y=sinx-|sinx| | B. | y=|sinx|+sinx | C. | y=|sinx| | D. | y=|sinx|-sinx |